În mod evident, minorii și cofactori pot diferi doar în semn.
Luați în considerare fără dovada unei importante teoremă - factor determinant Teorema de expansiune.
Factorul determinant este suma produselor de elemente ale unui rând sau o coloană în cofactori lor.
Folosind această teoremă, vom scrie extinderea determinant al treilea ordin în ceea ce privește prima linie.
.
În formă extinsă:
.
Această formulă poate fi utilizată ca determinant principal în calculul al treilea ordin.
Teorema de descompunere ne permite să reducem calcularea determinantului al treilea ordin la calcularea celor trei factori determinanți de ordinul al doilea.
Se recomandă să se stabilească determinant pentru rândul sau coloana în care există zero, deoarece zero elemente nu este necesară pentru a găsi cofactori.
Descompunerea teoremă oferă un al doilea mod de a calcula determinanții al treilea ordin.
EXEMPLE. Calculați determinantul folosind teorema de expansiune.
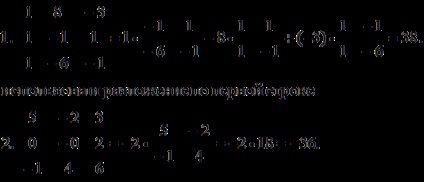
Am folosit o descompunere de-al doilea rând.
Descompunerea teoremă poate calcula, de asemenea, factorii determinanți de ordin superior, reducerea lor la calculul mai multor determinanți ai al treilea sau al doilea ordin.
De exemplu, un al patrulea factor determinant ordin poate fi redus la calculul celor patru determinanți ai treilea ordin.
Treia întrebare academică Cramer
Noi aplicăm analiza teoriei determinanților la sistemele de ecuații liniare de rezolvare.
1. Un sistem de două ecuații liniare cu două necunoscute.
a11. ..., a22 - coeficienții necunoscutelor, indexate de doi indici, în cazul în care primul indice indică numărul ecuației, iar al doilea index - un număr necunoscut.
Să ne amintim că o soluție de (3) este o pereche de valori x1, x2. care atunci când este substituit în ambele ecuații le transformă în adevărate egalitate.
În cazul în care sistemul are o soluție unică, această soluție poate fi găsită folosind identificatorul secundar.
DEFINIȚIE 5. Determinantul coeficienților de necunoscutele, se numește determinant al sistemului.
Notăm determinantul sistemului D.
.
Coloanele determinant D sunt coeficienți, respectiv, cu x1 și x2.
Vom introduce două d o p n și l adică l s n i x o p p e d l e și l adică eu care sunt derivate din sistemul de înlocuire determinant al unuia dintre coloanele membrilor liberi coloana:
.
Luați în considerare următoarea teoremă fără dovezi:
Cramer (pentru n = 2)
Dacă determinant D al sistemului (3) este diferit de zero (D¹ 0), sistemul are o soluție unică, care este dat de:
Formula (4) sunt formulele Cramer.
EXEMPLU. Rezolva sistemul de regula lui Cramer.

.
2. Sistemul de trei ecuații liniare cu trei necunoscute:
În cazul unui singur sistem de soluții (5) pot fi rezolvate prin utilizarea unui al treilea ordin determinanților.
Sistemul D Determinant are forma:
Introducem trei determinant suplimentar:
.
In mod similar teorema este formulată.
Cramer (pentru cazul n = 3)
Dacă sistemul determinant D (5) este non-zero, atunci sistemul are o soluție unică, care este dat de:
Formula (6) - este de formula Cramer.
NOTĂ. G. Kramer (1704 - 1752) - matematician elvețian.
Rețineți că teorema lui Cramer se aplică atunci când numărul de ecuații este egal cu numărul de necunoscute și când determinantul D este nenul.
Notă doar un singur caz:
Dacă determinantul sistemului este zero (D = 0), și cel puțin o determinanților suplimentari diferiți de zero, sistemul nu are soluții (adică este inconsistent).
Teorema lui Cramer poate fi generalizat la un sistem de n ecuații liniare în n necunoscute.
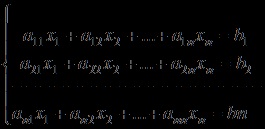
, singura soluție este pentru sistemul
obținută din determinant D, în cazul în care acesta este necunoscut coeficienții coloanei
xi înlocui coloana termenilor liberi.
Rețineți că factorii determinanți D, D1. .... Dn de ordinul n.