1.1. Un sistem de două ecuații liniare și identificatorul secundar
Să considerăm un sistem de două ecuații liniare cu două necunoscute:
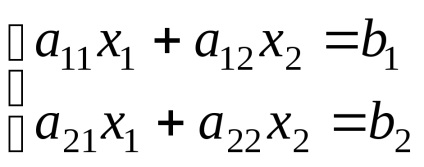
coeficienţii
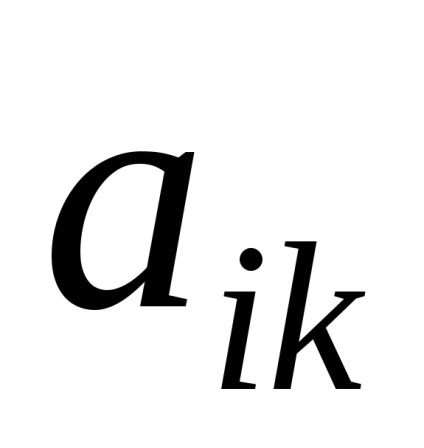
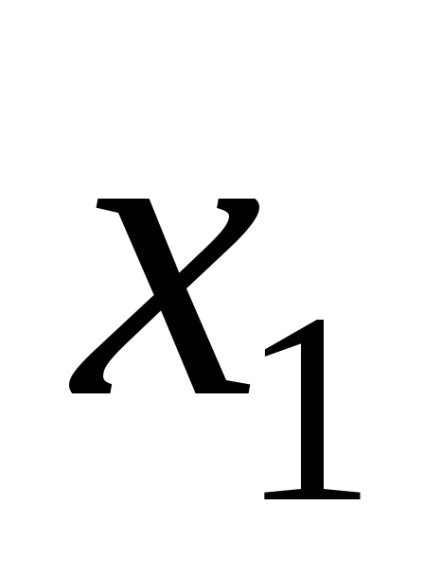
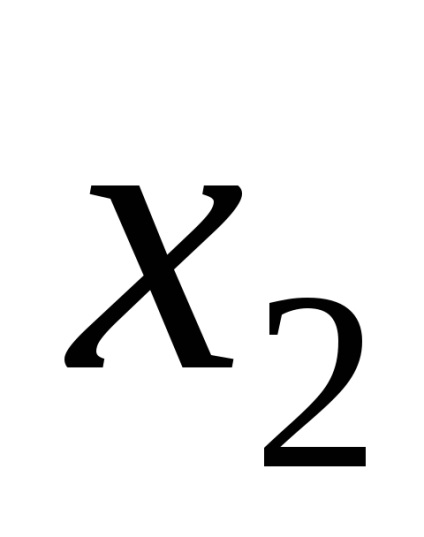
Principalul factor determinant al sistemului este numit un tabel al coeficienților de necunoscutele și închise în paranteze pătrate:

determinant Auxiliar este determinantul obținut din principalul determinant al înlocuirii unuia dintre coloanele din coloana termenilor liberi:
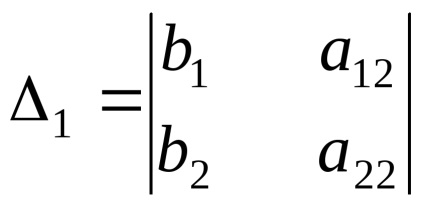
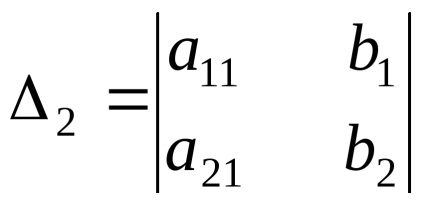
Principalul factor determinant diagonală - o direcție diagonală, din colțul din stânga sus în colțul din dreapta jos. Al doilea nazyvaetsyapobochnoy diagonală.
Determinantul ordinul al doilea este diferența dintre produsul elementelor diagonale ale produsului și elementele diagonale secundare:
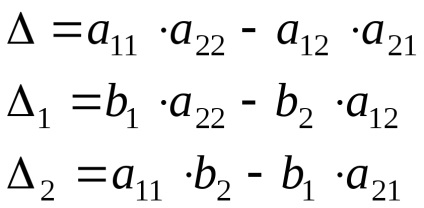
regula lui Cramer: Soluția este găsită prin împărțirea determinanților auxiliari ai determinant principal al sistemului
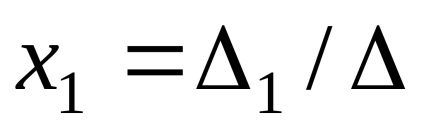
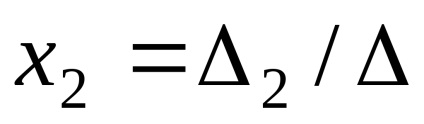
Nota 1: Utilizarea regula lui Cramer este posibilă în cazul în care determinantul sistemului

Observația 2. Formula Cramer generalizat la sistemele de ordin superior.
Exemplul 1: rezolva sistemul:
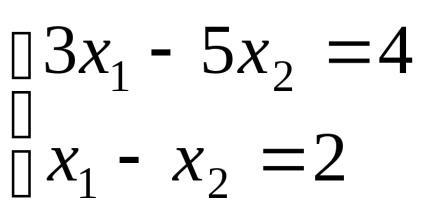
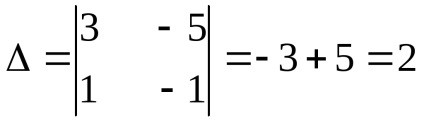
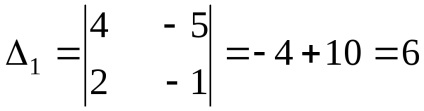
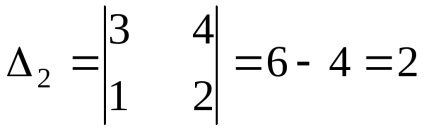
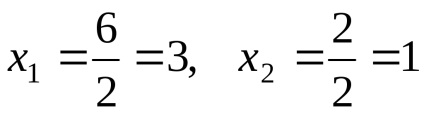
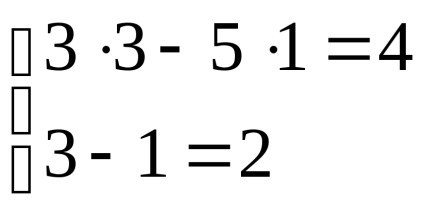
Concluzie: Sistemul este rezolvat corect :.
1.2. Un sistem de trei ecuații liniare și determinanții de ordinul trei
Luați în considerare un sistem de trei ecuații liniare cu trei necunoscute:
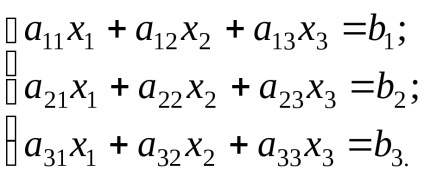
Determinantul coeficienților de necunoscutele, se numește determinantul sistemului sau determinantul principal:
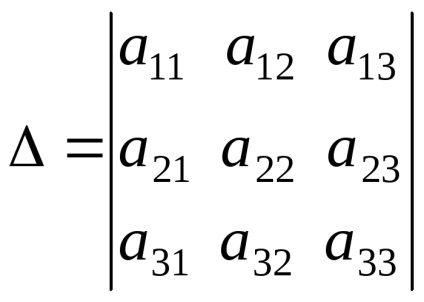
dacă

în cazul în care calificative
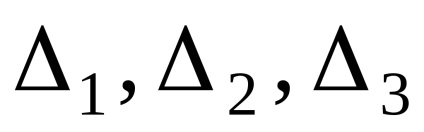

Exemplul 2. Rezolvați sistemul
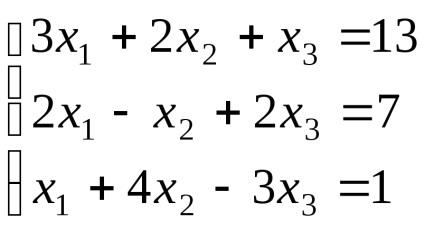
Vor forma determinanților principale și auxiliare:
Rămâne să ia în considerare regulile de calcul factorii determinanți ai treilea ordin. Trei: de obicei, adăugați coloane, regula lui sarrus, de obicei descompunere.
a) Regula alăturarea primele două coloane un identificator primar:
.
Calculele au fost efectuate după cum urmează: cu semnul său sunt un produs de elemente ale diagonalei principale și paralel cu acesta, cu semnul opus să ia lucrări ale elementelor diagonale secundare și paralel cu aceasta.
Luate cu elementele sale de lucru semn al diagonalei principale și paralele cu acesta, în care al treilea element de lipsă luate din unghiul opus. În taxa de semn contrar, funcționează elemente incidentale pe diagonală și paralele cu acesta, al treilea element este preluat din unghiul opus.
c) dreptul de expansiune în rândul elementelor sau coloana:
Factorul determinant este suma produselor elementelor din orice rând (coloană) la cofactori respective.
Cofactor - este determinantul unui ordin inferior, obținut prin ștergerea rândului corespunzător și coloanei, și ia în considerare semnul


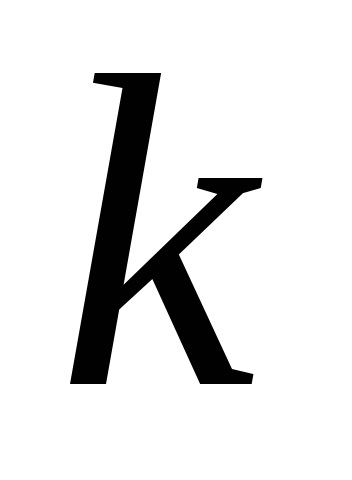
Calculăm această regulă determinanți auxiliare


După calcularea tuturor factorilor determinanți, regula lui Cramer găsim variabilele:
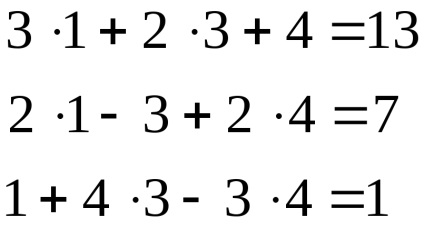
Concluzie: Sistemul este rezolvat corect :.
Proprietățile de bază ale determinanților
Trebuie amintit faptul că determinantul - acel număr. găsit de niște reguli. Calculul său poate fi simplificată, dacă vom folosi proprietățile de bază, care sunt valabile pentru factorii determinanți ai orice ordine.
Proprietatea 1. Valoarea determinantului nu se schimba prin înlocuirea tuturor coloanelor sale de linie rândul corespunzător și vice-versa.
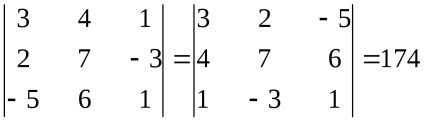
Operația înlocui coloanele siruri se numește transpunere. Această proprietate implică faptul că orice declarație este valabilă pentru determinantul liniilor, este corect și pentru coloanele sale.
2. Proprietatea, semnul determinantului se va schimba la opusul Dacă în doi rând determinant swap (coloana).
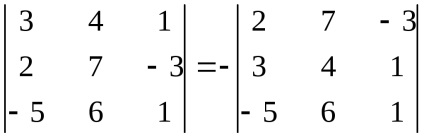
Proprietatea 3. În cazul în care toate elementele de orice rând a determinantului egal cu 0, determinantul este egal cu 0.
4. În cazul în care linia de proprietate a elementelor determinante înmulțit (împărțite) cu privire la orice număr
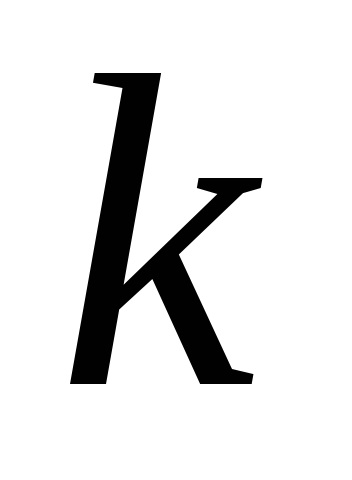
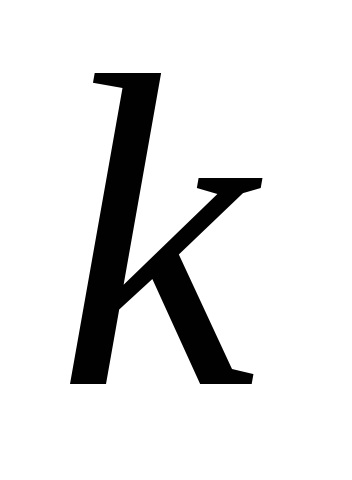
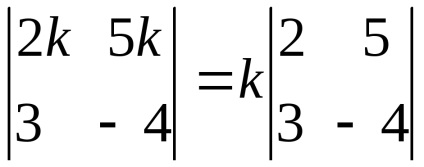
În cazul în care elementele unor rânduri au un factor comun, atunci acesta poate fi luat ca un semn al determinantului.
5. Dacă determinantul proprietate are două egale sau proporțională cu linie, astfel determinant este egal cu 0.
Proprietatea 6. În cazul în care elementele unora dintre liniei determinant reprezintă suma a doi termeni, determinantul este egală cu suma a doi factori determinanți.
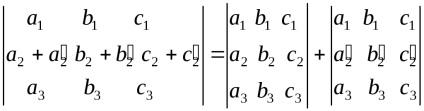
7. Valoarea proprietății determinantului nu se schimba în cazul în care elementele de orice rând pentru a adăuga elemente de un alt rând, înmulțit cu același număr.
Acest factor determinant adăugat inițial la a doua linie de o treime înmulțit cu 2 și apoi scade din coloana a treia din al doilea, apoi al doilea rând adăugat la prima și a treia, pentru a obține mai multe zerouri conta și simplificate.
transformări elementare sunt numite factor determinant simplifica-l prin utilizarea acestor proprietăți.
Exemplul 1. Se calculează determinant

count directă a uneia dintre regulile discutate mai sus conduce la calcule greoaie. Prin urmare, este recomandabil să se utilizeze proprietățile:
a) I-linie scade a doua înmulțit cu 2;
b) scăderea din treimea II linia înmulțită cu 3.
Rezultatul este:

Descompunem acest determinant de elementele primei coloane, conținând doar un element nenul.
.
Sistem și factorii determinanți ai ordinelor superioare
sistem
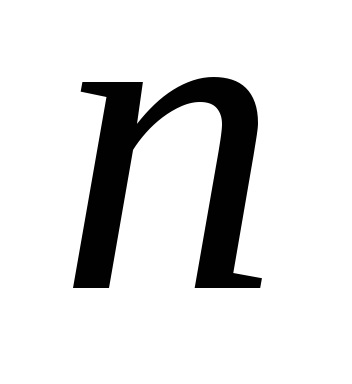
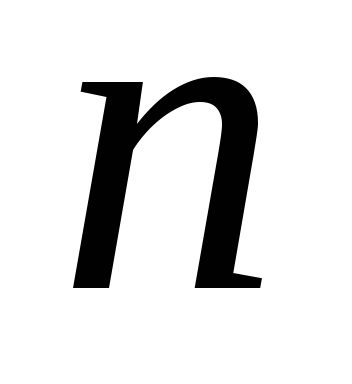
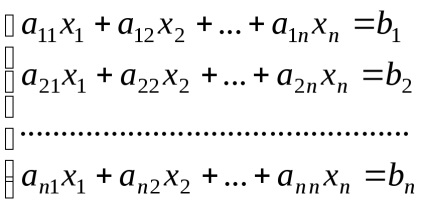
Pentru acest caz, puteți face, de asemenea, determinanții principale și auxiliare, precum și pentru a identifica necunoscutul prin regula lui Cramer. Problema este că determinanții de ordin superior pot fi calculate numai prin reducerea ordinii și reducerea lor la factorii determinanți ai treilea ordin. Acest lucru se poate realiza prin expansiune directă în rânduri sau coloane de elemente, iar preliminarii prin transformări elementare, și descompunerea ulterioară.
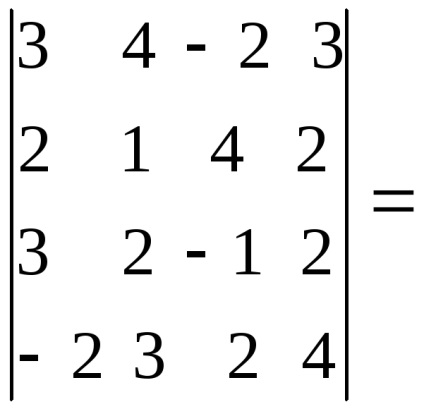
Exemplul 4. Se calculează determinant fourfold

Soluția se găsește în două moduri:
a) prin descompunerea directă a elementelor din primul rând:
b) prin transformări preliminare și descompunerea ulterioară