4. Soluția problemei
4.1. Ecuațiile diferențiale ale primului ordin
cu variabile separabile
Soluție generală Exemplul 1. Hayti ecuației y ¢ cosx - (y + 1) sinx = 0.
Decizie. Se separă variabilele. Pentru a face acest lucru, vom multiplica ambele părți de multiplicare, înlocuind y ¢ pe ecuația devine:
Vom integra acest termen ecuație de termen, obținem:
,
Am primit o ecuație integrală generală.
Exemplul 2. Găsiți soluția particulară a ecuației: dacă y = 3, atunci când x = 1.
Decizie. Rescriem ecuația în forma: 2ydy = (1 - 3x 2) dx. înlocuind y ¢ pe
Integrarea ambele părți ale ecuației, obținem:
- ecuația generală integrală. Substituind condițiile inițiale la y = 3 x = 1, obținem:
9 = 1 - 1 + c. rezultă că c = 9. Soluția particular necesară are forma:
4.2. ecuații diferențiale omogeni
prima comandă
Exemplu. Integrați ecuația: 2x 2 dy = (x 2 + y 2) dx.
Decizie. Impartind ambele fețe cu 2 x dx. obținem ecuația, partea dreapta a care este o funcție a relației:
Pune în ea, atunci y = ux. Ne diferentiem obține o ecuație cu mai multe variabile:
.
După separarea variabilelor obținem ecuația cu variabile separate:
.
Integrarea substitut, obținem:
Notă. În separarea variabilelor separam de x și (u - 1) 2, care este posibilă numai dacă x ¹ 0 și u ¹ 1. Testul imediat este ușor de văzut că x = 0 și u = 1, adică y = x ... Ele sunt, de asemenea, soluții ale acestei ecuații, dar ele nu sunt incluse în integralei generală. Astfel de soluții sunt numite speciale.
4.3. Ecuatii diferentiale liniare
prima comandă
Exemplul 1. Găsiți soluția generală a ecuației :.
Decizie. Se împarte ambele părți ale acestei ecuații de (1 + x 2), obținem:
- ecuație liniară. Am rezolva prin utilizarea metodei de substituție y = u × v. apoi înlocuiți valoarea ¢ y și y în această ecuație:
,
Alegeți o funcție v astfel încât expresia din paranteze este egală cu zero:
.
Apoi, (4.1) poate fi scrisă sub forma unui sistem de ecuații:
Vom găsi o funcție v din prima ecuație:
,
.
Integrarea, obținem, să c1 = 1, v = 1 + x 2.
Înlocuim valoarea lui V în a doua ecuație a (4.2):
Punctul de u și v sunt substituite în ecuația y = u × v. obținem:
- soluția generală a acestei ecuații.
Luați în considerare problema, rezultând într-o ecuație diferențială.
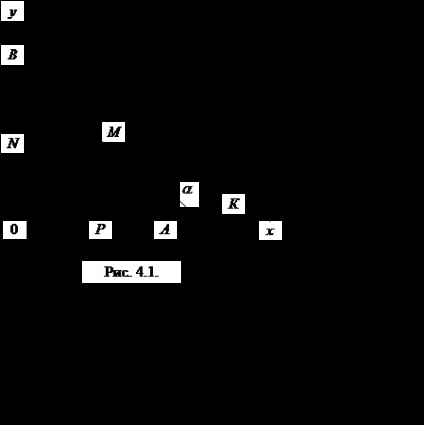
Exemplul 2. Găsiți o curbă care trece prin punctul M0 (1, 4) și având proprietatea că orice segment al tangentei sale, inclus între axele de coordonate, este împărțit în două la punctul de tangență.
Decizie. Vom face desenul (Fig. 4.1). Fie M (x, y) - un punct arbitrar al curbei dorite, AB - segment tangent curbei în acest moment cuprins între axele de coordonate. Prin ipoteză, BM = sarcină MA. În cazul în care PO - abscisa punctului M. UMEDĂ
.
Cu toate acestea, PA = OP. prin urmare, că OA = 2x. OB = 2y.
Pe de altă parte, din moment ce
.
În consecință, - diferențiale ecuații cu variabile separabile. Împărțim variabilele care integrează:
, .
Deoarece curba trebuie să treacă prin punctul M0 (1, 4), apoi substituind coordonatele sale în această ecuație, obținem: 1 x 4 = c. c = 4. Astfel, curba dorită definită de ecuația.
Exemplul 3. Marine retardati propunerea sub efectul de rezistență la apă, care este proporțională cu viteza barca. Incepand cu barca de 1,5 m / s prin 4 cu rata de 1 m / s. Găsiți barca de viteză în 12 secunde după începerea mișcării.
Decizie. Conform celei de a doua lege a ecuației dinamicii diferențiale a mișcării este după cum urmează:
Această ecuație diferențială cu variabile separabile. Separarea variabilelor, obținem:
,
Substituind condițiile inițiale, vom găsi:
În consecință ,. Valoarea k / m este definită prin substituirea a doua condiții inițiale: t = 4, v = 1 ,. Rezultă: Astfel, avem o soluție particulară a ecuației:
.
Substitut în această ecuație t = 12, în final obținem:
.
4.4. Ecuații diferențiale de ordin superior,
permițând reducerea ordinului
Exemplul 1. Integrarea ecuației.
Decizie. Integrarea acestei ecuații de două ori consecutiv:
Exemplul 2. Găsiți soluția generală a ecuației:
Decizie. Această ecuație nu conține în mod explicit functia y dorită. Punerea în ecuația y ¢ = z. y ² = z ¢, obținem o ecuație de ordinul întâi liniară în raport cu z (x) :. Înlocuirea z = uv, z ¢ = u ¢ v + uv ¢, obținem:
Această ecuație va înlocui sistemul de ecuații:
.
Rezolva prima ecuație:
Noi integra: c0 = 0, sau să înlocuiască valoarea găsită pentru v în a doua ecuație :. Divide integra variabile: de aceea Revenind la variabila y originală. obținem:
.
Împărțim variabilele care integrează:
soluția generală a acestei ecuații:
Exemplul 3. Găsiți soluția generală a ecuației:
Decizie. Această ecuație diferențială nu conține în mod explicit variabila x independent. Să y ¢ = p. y ² = p (dp / dy), înlocuind în această ecuație:
Noi separa variabilele integrate sau:
, .
Deoarece p = ¢ y, obținem y ¢ = c1 (3 + y) - ecuație de ordinul I cu variabile separabile. Noi le despart: integrarea:
, , .
O soluție generală a acestei ecuații.
4.5. Ecuatii diferentiale liniare
Pentru a doua
cu coeficienți constanți
Pentru a găsi o anumită soluție de ecuații liniare neomogene folosind metoda coeficienților nedeterminat. O soluție particulară a ecuației liniare neomogene pentru laturile din dreapta de un tip special, poate fi găsit prin referire la dreapta. Scris în tabelul din cele mai frecvente cazuri (Tabelul 4.1.).
Partea dreaptă a ecuației diferențiale
Rădăcinile caracteristicii
ecuație