
Acasă | Despre noi | feedback-ul
Luați în considerare cazurile cele mai simple de ecuații diferențiale de ordinul al doilea, care permit reducerea ordinului.
1. Cea mai simplă ecuație de acest tip este ecuația:
,
adică ecuația, partea dreaptă depinde numai de variabila independentă. Integrarea ambele părți ale ecuației, obținem. în cazul în care - integrarea arbitrară.
Astfel, a doua ecuație diferențială are mai multe soluții. După cum sa menționat mai sus, pentru a găsi o soluție special, de necesitatea de a satisface condițiile inițiale, care este de a defini arbitrar
Decizie. Deoarece. atunci. adică. Apoi. Astfel.
Integrarea ambelor părți ale acestei expresii, obținem soluția generală a ecuației inițiale.
Exemplul 2: găsi o soluție particulară. care îndeplinește condițiile inițiale. .
Mai întâi căutăm soluția generală. această ecuație trebuie să se integreze în mod consecvent. Având în vedere că
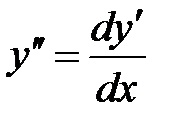
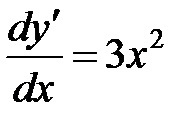
Inmultiti pe ambele părți ale ecuației. integra
.
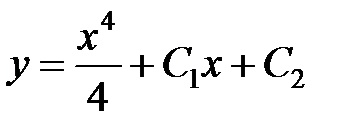
Acum, trebuie să găsiți și având în vedere condițiile inițiale. Prin ipoteză, și apoi
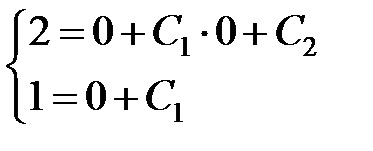
Prin urmare. . atunci
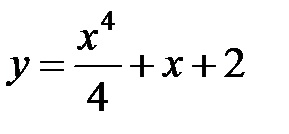
2. Ecuația diferențială care permite o reducere a comenzii, tipul :.
Partea dreaptă a ecuației nu conține funcția necunoscută. În acest caz, ecuația poate fi rezolvată prin substituirea:
. .
Ca rezultat al acestei ecuații de substituție devine :. că este, ordinea sa este redusă. De aceea, am comanda ecuație diferențială.
Decizie. Deoarece ecuația nu conține funcția necunoscută. apoi soluțiile sale folosim de substituție: și. Atunci obținem:
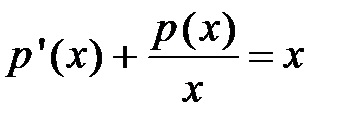
Asimilarea expresia care stă în ultima ecuație între paranteze la zero, obținem:
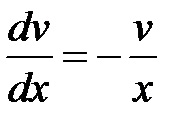
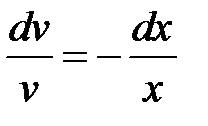
Integrarea ambelor părți ale ultimei relației obținem. Prin urmare, pentru a găsi funcția de necunoscut avem ecuație diferențială:
Astfel, funcția este egală cu :. Acum vom găsi funcția.
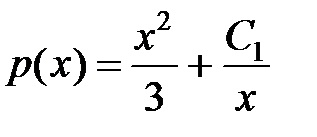
Deoarece. atunci avem :.
Mai mult, prin integrarea ambele părți ale acestei ecuații, vom obține soluția finală a ecuației inițiale:
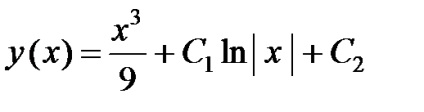
Exemplul 4. Găsiți soluția generală.
Decizie. Aplicare de înlocuire. în cazul în care. După aceea, ecuația devine :. Ecuația obținută cu variabile separabile
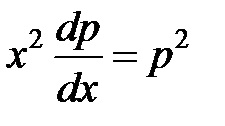
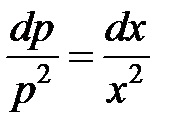
Noi luăm integralei ambele părți
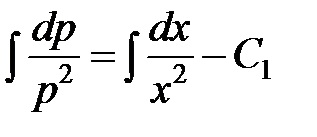
Având în vedere că avem
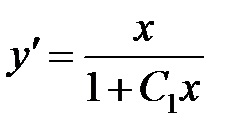
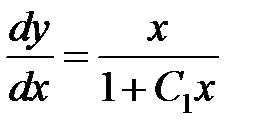
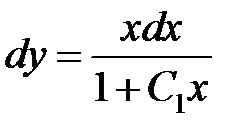
Integrarea ambele părți ale acestei ecuații
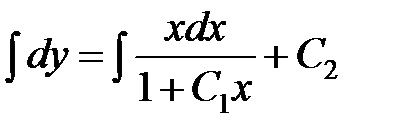
pentru a găsi
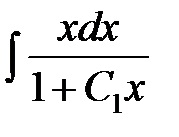
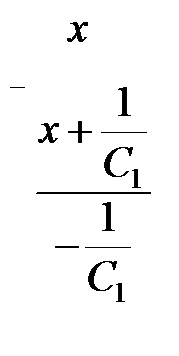
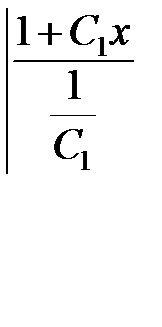
Integral ia forma
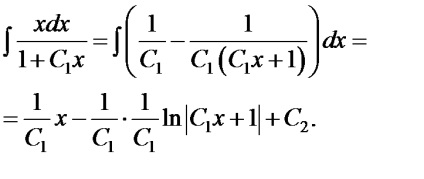
.
3. Ecuația care nu conține argumentul. Partea dreaptă a ecuației, în acest caz nu conține variabila independentă și soluția poate fi obținută prin substituirea:
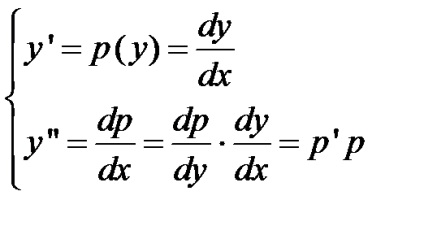
Substituind funcție necunoscută și derivatul său la ecuația inițială, ecuația diferențială a primului ordin ca funcție de:
.
Și desemnând și substituind aceste expresii în ecuația inițială, obținem: - ecuație diferențială cu variabile separabile. Separarea variabilelor, obținem:
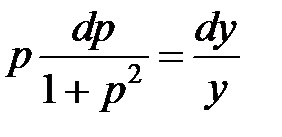
Integrarea ambelor părți ale acestei ecuații, obținem integralei totală a ecuației diferențiale inițiale:
.