Obiectiv: o determinare experimentală a modulului de elasticitate al plăcilor realizate din diferite materiale, metoda de îndoire.
Dispozitive și accesorii: instalarea „modulul lui Young“, plăci, set de sarcini cu o greutate de 0,05 kg, 0,1 kg și 0,15 kg.
Elemente de teoria și metoda experimentală
Diferitele elemente ale structurilor și mașini au adesea numai forțe longitudinale care duce la o întindere sușă sau compresiune.
Savantul englez Robert Guk din secolul XVII a descoperit legea fundamentală între forțele și mișcările cauzate de acestea, stabilirea proporțional alungirea eșantionului forței de tracțiune.
Savantul englez Thomas Young a secolului al XIX-lea, pentru prima dată și-a exprimat ideea că există o constantă pentru fiecare material care caracterizează capacitatea sa de a rezista presiunilor exterioare. Conceptul de o asemenea magnitudine, pe care el a numit (mai târziu „modulul lui Young“), „modul de elasticitate“ a fost formulată în 1807, în lucrarea sa „Filosofia naturală“.
Modulul de elasticitate descrie cea mai importantă proprietate a unui material structural - rigiditate - și este un concept fundamental, fără de care nu se poate face nici un calcul de inginerie de elemente și structuri structurale. Fig. 1 prezintă o tijă cu o axă rectilinie sub acțiunea forțelor longitudinale N, unde
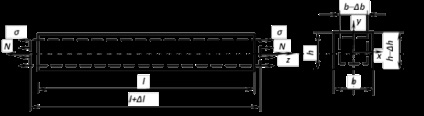
# 963; - tensiune normală,
A - aria de secțiune transversală a tijei.
Fig. 1. deformație longitudinală și transversală a tijei
Sub acțiunea forțelor longitudinale deformate tijă. În cazul în care se extinde, crește lungimea sa și devine egală cu L + # 8710; L. unde # 8710; L - este deformarea longitudinală absolută (alungire) a tijei. Dimensiunile transversale ale sale reduse și să ia valori H # 8710; H și B- # 8710; B. unde # 8710; H și # 8710; B - este absolut deformarea transversală a tijei.
Raportul dintre deformarea longitudinală absolută a tijei la lungimea sa inițială se numește deformarea longitudinală relativă:
Raportul dintre deformarea laterală absolută a tijei la dimensiunea sa inițială transversală numită deformarea transversală relativă:
Aici semnul „+“ la tulpina și semnul „-“ în deformațiile și livrate deoarece dimensiunile longitudinale de tracțiune ale tijei sunt mărite, iar scăderea transversală.
Ultimul pas în formarea legii lui Hooke în forma sa actuală de către matematicianul francez Cauchy, care în 1822 a introdus în literatura de specialitate conceptul de „stres“ și „tulpina“, un om de știință francez și Navier, care în 1826 a dat definiția modulului de elasticitate ca raportul dintre sarcina per unitate de arie a secțiunii transversale a alungirii, care a produs
În cazul în care E - modulul Young (modulul de elasticitate al primului tip).
Astfel, legea Hooke primită aplicarea practică în forma de formula
Modulul de elasticitate E al materialului este o constantă fizică și este determinată experimental. Valoarea sa este exprimat în aceleași unități ca și tensiunea # 963;., M E. In pascali (Pa), ca # 949; - o cantitate adimensional. Modulul de elasticitate al majorității materialelor are valori numerice mari, și este de obicei exprimat în gigaPa (GPa).
Valoarea absolută a raportului sușei transversală în raport și tulpina longitudinală relativă la întindere sau compresiune în sfera de aplicare a legii Hooke se numește raportul Poisson
Acest coeficient adimensional care caracterizează proprietățile materialului și determinate experimental. El este numit după savantul francez, care l-a prezentat mai întâi la teorie.
După aplicarea la corpul extern incarca mutarea lui punct. De obicei amplitudinea deplasării elastice presupusă a fi mică în comparație cu dimensiunile geometrice ale corpurilor deformabile. Să considerăm, de exemplu, deplasarea unei grinzi în consolă de lungime L, cu încorporarea externă unilaterală în Fig. 2. Capătul liber al grinzii este aplicată forța concentrată F. care provoacă deformarea punctelor sale. Deformarea fasciculului în această secțiune denotă # 948;. Isolate element de volum Dz lungimea fasciculului. la Z distanță de capătul fix.
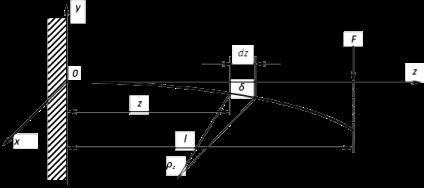
Fig. 2. Curbare grinzii în consolă
Statul deformat în secțiunea curentă a fasciculului este descrisă de raza de curbură sau curbura axei sale curbate.
Este cunoscut [2] că ecuația axei îndoite a grinzii are forma:
Unde IX - momentul de inerție axial
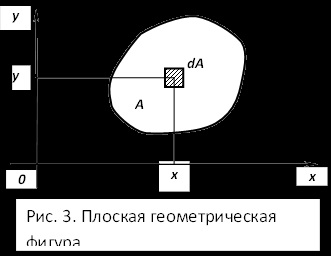
Fig. 3 prezintă o secțiune transversală arbitrară este o figură geometrică plană a cărei zonă A. distinge pe aceasta zona elementară DA.
Definim un moment secțiune transversală dreptunghiulară de inerție în raport cu axa CX și CY. trecând prin centrul său, așa cum se arată în Fig. 4.
Se împarte zona de dreptunghi în dreptunghiuri elementare cu dimensiunile B și Dy. acea zonă. Substituind valoarea în expresia (9) și integrarea, obținem:
Luați în considerare o lungime fascicul L. montate pe două suporturi și încărcate așa cum este prezentat în Fig. 5.
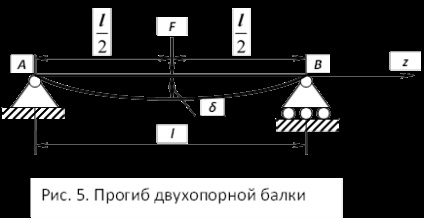
Soluția ecuației diferențiale (8) poate fi obținut prin integrarea succesivă. Când sarcina exterioară este situată simetric în raport cu suporturile, așa cum se arată în Fig. 5, soluția acestei ecuații [2] devine:
Prin urmare, modulul lui Young este definit prin formula
În ceea ce privește expresia (10) obținem
În consecință, definirea F sarcină și valoarea săgeții # 948; la grindă (placa) de lungime L cu dimensiunile transversale ale secțiunilor B și H. formula (14) se poate calcula modulul lui Young al materialului din care este făcută.
Descrierea configurării experimentale
Reprezentarea schematică a instalației „modulul lui Young“ este prezentată în Fig. 6.
Setarea „modulul lui Young“ constă dintr-o bază 1 pe care este fixat la fața birou 2. colțarul Situat 3 cu două suporturi prismatice 4. Pe suportul 5 este instalat proba (wafer). Cu proba 7 dispozitivul de încărcare, care este un suport de suport prismatic, atașat la proba dial-sarcină 6 și indicatorul 8 oră.
Ordinea de performanță
1. Așezați una dintre plăcile de testare pe suportul prismatică 4.
2. Setați indicatorul ora 8, astfel încât vârful atins placa.
3. Hang dispozitiv clemă 7 în mijlocul plăcii.
4. Atașați etrierul O masă M1 = 0,1 kg.
5. La un indicator scală 8 determină valoarea plăcii deflecție # 948; 1.
Hang etrierul 7. O masă M2 = 0,15 kg.
8. La un indicator scală 8 determină valoarea plăcii deflecție # 948; 2.
9. Se calculează F sarcinii prin formula
În cazul în care G - accelerația gravitațională.
10. Valoarea plăcilor de deflexie definite ca
11. Găsiți modulul lui Young prin formula (14), unde L = 0,114 m - distanța dintre prisme (lungime a plăcii); B = 0,012 m - lățimea secțiunii transversale a plăcii; H = 0,0008 m - grosimea plăcii; # 948; - valoarea plăcilor de deflexie, m.
12. Efectuați etapele cu o a doua placă de mai sus.
13. Se repetă pentru ambele arcuri revendicări. 1-12 de două ori mai multe.
Materialul probelor - arcuri din oțel și bronz.
Explicați rezultatele obținute plăci moduli elastice, le compară cu datele de referință [3, 4].
Procedura de evaluare a erorilor
Să presupunem că valorile de evaluare de eroare ale modulului lui Young cu formula (14) este determinată de eroarea de măsurare lungimii plăcii L (eroarea sistematică) și eroarea de deflexie estimările d (sistematică + eroare aleatoare).
Înregistreze rezultatele măsurătorilor directe ale parametrilor de mai sus:
B) d =
Înregistreze rezultatele măsurătorilor indirecte:
Întrebări și sarcini de auto-control
1. Ce este diferit de stresul normal al tangenta?
2. Care sunt formule pentru a determina deformarea absolută și relativă?
3. Care este valoarea primului tip este numit un modul de elasticitate?
4. Cum este raportul Poisson?
5. Ce este o secțiune de rigiditate de îndoire?
6. Care este formulele diferență momentului de inerție axial în raport cu axele Ox și Oy?
7. Ce formulă exprimă deformării grinzi dublu-sprijinite?