30. repetate de testare independente. formula Bernoulli. exemple
Testele independente repetate menționate teste care îndeplinesc următoarele condiții:
1) Numărul n curs de testare;
2) probabilitatea unui eveniment aleatoriu în fiecare dintre teste este constantă:
Exemple retestare:
1) extragerea mai multor coșuri de minge, cu condiția ca mingea luată după înregistrarea culoarea este pus înapoi în cutie;
2) repetarea unuia fotografii shooter de pe aceeași țintă, cu condiția ca probabilitatea unei lovituri de succes este primit aceeași pentru fiecare lovitură (rolul de aducere la zero nu este considerată).
În cazul în care probabilitatea de apariție a unui eveniment în fiecare studiu este constantă, atunci probabilitatea ca evenimentul are loc exact o dată în studii independente, este :. în cazul în care.
Exemplu. Probabilitatea de a lovi ținta într-o singură lovitură este egală cu 0,7 și nu depinde de numărul împușcat. Găsiți probabilitatea ca la 5 fotografii vor fi exact 3 lovind ținta.
Decizie. Membru supleant în formula lui Bernoulli pentru aceste sarcini și a obține:
31. Conceptul de teoremei limită centrală. Teorema locale și integrale Moivre-Laplace, condițiile de aplicabilitate a acestora. Exemple.
Teorema limită centrală este un grup teoremă. dedicat stabilirii condițiilor în care există o distribuție normală. Printre aceste teoreme un loc important aparține teorema lui Lyapunov.
Legea distribuției sumelor de variabile aleatoare independente (i = 1,2, \ ldots, n) „align = lățimea inferioară = 147 height = 18 border = 0> este aproape de o distribuție normală cu o creștere infinită, dacă sunt îndeplinite următoarele condiții .:
toate valorile au așteptări matematice finite și varianța:
nici una dintre valorile valorii nu în mod dramatic diferită de restul:
În rezolvarea multor probleme practice, folosind următoarea formulare teorema lui Lyapunov pentru media aritmetică a valorilor observate ale variabilei aleatoare. care este, de asemenea, o variabilă aleatoare (în acest caz, sunt îndeplinite două condiții):
în cazul în care dispersia ozhidaniyai matematică finită velichinaimeet aleatoare, mediul de distribuție
aritmetică, calculată din valorile observate ale unei variabile aleatoare procese vnezavisimosti pripriblizhaetsya la distribuția normală cu dispersie ozhidaniemi medie, adică,
Prin urmare, probabilitatea ca este conținută în interval. Acesta poate fi calculat prin formula
Utilizarea funcției Laplace poate fi scrisă într-o formă convenabilă de calcule:
Trebuie remarcat faptul că teorema limită centrală deține nu doar continuă, ci și pentru variabile aleatoare discrete. Semnificația practică a teoremei lui Lyapunov este imens. Experiența arată că legea de distribuție a sumei de variabile aleatoare independente, comparabile în disiparea, se apropie rapid normală. Chiar și atunci când numărul de termeni de ordinul a zeci de distribuție suma de drept poate fi schimbat la normal.
32. * Consecințele teoremei integrală a de Moivre-Laplace. Exemplu s.
Sledstvie.Esli veroyatnostnastupleniya sobytiyav fiecare proces este constant și diferit de 0 și 1, atunci pentru probabilitate suficient de mare de testare chislenezavisimyh. că:
a) un număr m de apariții ale proizvedeniyane sobytiyaotlichaetsya mai mult decât suma (în valoare absolută), adică. ;
b) în cadrul chastostsobytiyazaklyuchena otdo (inclusiv), adică
c) din chastostsobytiyaotlichaetsya sale veroyatnostine mai mult decât suma (în valoare absolută), adică
Exemplu. Probabilitatea evenimentului A în fiecare din cele 900 de studii independente este egală. Găsiți probabilitatea ca evenimentul A are loc: a) 710 de ori; b) de la 710 până la 740 de ori.
a) Având în vedere. Din moment. utilizarea formulelor 24-26, funcții de paritate și tabelul 1 din anexă [4 s.553-554], obținem:
b) Având în vedere. Din moment. utilizarea formulelor 27-29, funcția impar și tabelul 2 din anexa [4, s.555], obținem:
Răspuns: a) 0,0236; b) 0.7993.
33. asimptotic cu formula Poisson și condițiile aplicabilității acesteia. Exemple.
Aplicarea formulei lui Bernoulli pentru valori mari ale produsului conduce la un număr foarte mare și foarte mici (și), care este rău din punct de vedere computational, deci trebuie să folosim formule asimptotice aproximative.
Luați în considerare situația în care numărul de încercări în Bernoulli crește schema fără limită, și probabilitatea de apariție a unui eveniment în fiecare studiu tinde la zero, în așa fel încât produsul rămâne o valoare constantă, care este notat. În acest caz, următoarea relație deține:
Dovada. Conform formulei Bernoulli
Noi folosim faptul că starea sau Bernoulli cu formula și ia forma:
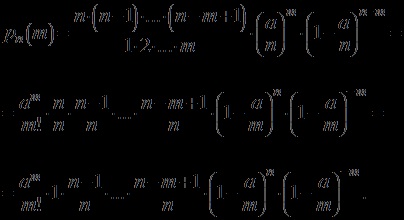
Deoarece atât fix și tinde la infinit, atunci factorii; ...; și să depună eforturi pentru unitate și factorul tinde să. l
expresie aproximare Poisson primită se numește formula Bernoulli. Această formulă oferă o bună aproximare pentru mari și mici suficient (de exemplu, u).
Probabilitatea evenimentului constă în faptul că nu va fi nici mai mult timp, în mod evident, se calculează conform formulei
Exemplu. Întreprinderea a produs și a trimis la client 100.000 de sticle de bere. Probabilitatea ca sticla poate fi un liliac. este egal cu 0,0001. Găsiți probabilitatea ca în administrarea partidului va fi exact trei sau exact cinci sticle sparte.
Decizie. Având în vedere prin: n = 100000, p = 0,0001, m = 3 (m = 5).
Folosind formula Poisson
34. Lema Cebîșev. exemple
În studiul teoriei probabilității este necesar să se utilizeze conceptul unui eveniment aleator și variabila aleatoare. În acest caz, rezultatul testului prezis în avans, în care pot apărea sau nu apar sau că un eveniment sau orice valoare particulară a variabilei aleatoare, este imposibil, deoarece rezultatul testului depinde de mai multe motive aleatorii, nu identificabile.
În studiul rezultatelor observațiilor fenomenelor reale de masă întâmplătoare, deoarece există unele modele. Se atrage atenția asupra faptului că acestea au proprietatea de stabilitate. Esența acestei proprietăți constă în faptul că caracteristicile specifice ale fiecărui fenomen aleatoriu individ aproape nici un efect asupra rezultatului mediu al masei mari a unor astfel de fenomene, precum și caracteristicile de evenimente aleatorii și variabile aleatoare observate în studiile. la creșterea nelimitată a numărului de teste sunt greu aleatoare.
Teorema legii numerelor mari să stabilească relația dintre șansă și necesitate.
Teorema lui Cebîșev: un număr suficient de mare de variabile aleatoare independente X1. X2. X3. Xn. variația fiecăreia dintre care nu depășește unul și același număr constant de B, pentru orice număr de inegalitate număr arbitrar mic
Rezultă din teorema că media aritmetică? Unele variabile aleatoare, cu o creștere a numărului acestora arată stabilitatea proprietății, adică. E. Tinde în probabilitate la o valoare nonrandom, care este media aritmetică a așteptărilor acestor variabile, adică, probabilitatea de deviere a valorii absolute a mediei aritmetice a valorilor aleatoare din media aritmetică a așteptărilor lor matematice mai mică decât sub creștere nelimitată de n tinde la 1, adică este aproape sigur eveniment.
Să considerăm cazul special al teoremei lui Cebîșev:
Să presupunem că există n încercări n valori ale variabilei aleatoare X, având așteptări M (X) și dispersia D (X). Valorile obținute pot fi considerate ca variabile aleatoare X1, X2, X3. Xn,. Trebuie să se înțeleagă acest lucru. O serie de teste efectuate în mod repetat n. Prin urmare, ca rezultat al testului i-lea, i = l, 2, 3. n, o serie de teste apar kayvvvvzhdoy o anumită valoare a variabilei aleatoare X, nu este cunoscut în prealabil. Prin urmare, i-e a aleatoare xi valoarea variabilei, primită în proces i-lea, se schimbă în mod aleatoriu, în cazul în care trecerea de la un lot de test la altul. Astfel, fiecare xi valoare poate fi considerată o variabilă aleatoare Xi.
Să presupunem că testele îndeplinesc următoarele cerințe:
1) Testele sunt independente. Acest lucru înseamnă că rezultatele X1, X2, X3. Xn să fie independent aleatoare valoare test;
2) Testele sunt efectuate în aceleași condiții, acest lucru înseamnă că, în ceea ce privește teoria probabilității ca fiecare dintre variabile aleatoare X1, X2, X3. Xn are aceeași lege de distribuție ca valoare inițială a X, prin urmare, MXI = MX și DXi = DX, i = 1, 2. n.
Având în vedere condițiile de mai sus, obținem
Trecerea la limita, avem
Din acest din urmă ecuație rezultă că media aritmetică a unei variabile aleatoare X are proprietatea de stabilitate.
Teorema lui Cebîșev este de mare folos în practică. Acesta permite utilizarea mediei aritmetice, pentru a obține o idee de magnitudinea de așteptare. și vice-versa. Astfel, prin măsurarea unui parametru cu dispozitivul, neautorizarea eroarea sistematică se poate obține un număr suficient de mare de măsurări, aritmetică, care prin Teorema Cebîșev, practic, nu va fi diferită de valoarea reală a unui parametru.
Exemplu. Să presupunem că, ca rezultat al testului de 100 independente aleatoare variabile X1 obținute. X2. ..., X100, cu egal matematic așteptările M (X) = 10 și egal varianțe D (X) = 1. probabilitatea Rate ca media aritmetică a valorilor aleatoare se abate de la valoarea absolută a lui M (X) este mai mică de 1/2.
Există un caz special de teorema lui Cebîșev. Aplicarea inegalității corespunzătoare pentru probabilitatea, obținem: