Aleatoare X variabilă este distribuit conform legii de distribuție exponențială cu parametrul λ. în cazul în care densitatea de probabilitate este dată de:
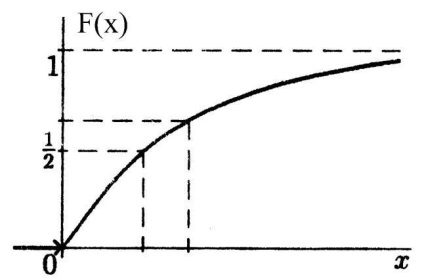
Funcția de distribuție este:
Așteptările și varianța pentru o variabilă aleatoare distribuită în conformitate cu o lege exponențială, sunt date de:
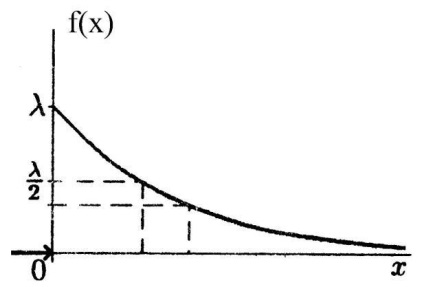
Sa constatat că timpul de reparație TV este o variabilă aleatoare X. distribuite exponential.
Se determină probabilitatea ca repararea TV va necesita cel puțin 20 de zile, în cazul în care timpul mediu pentru a repara televizoare este de 15 zile. Găsiți funcția de distribuție a densității de probabilitate și deviația standard a variabilei aleatoare X.
Prin ipoteză, așteptarea M (x) = 1 / λ = 15, unde parametrul X = 1/15. Apoi, funcția de densitate de probabilitate, iar distribuția va lua forma:
probabilitate dorită P (X ≥20) poate fi găsit de formula, prin integrarea densității de probabilitate, adică
dar este mai ușor de a face acest lucru folosind funcția de distribuție:
Am găsit abaterea medie: sigma (X) = M (X) = 15 zile.
dreptul de distribuție 3.Ravnomerny.
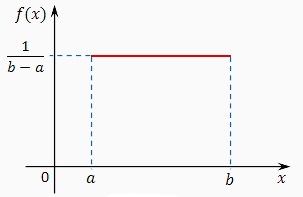
Continuu variabilă aleatoare X are o lege de distribuție uniformă (legea densitate constantă) pe un segment [a; b], în cazul în care, în acest moment, în funcție de densitate de probabilitate variabilă aleatoare este constantă, adică
Prin urmare, așteptarea unei variabile aleatoare uniform distribuite pe intervalul (a. B), egal cu mijlocul acestui interval.
Varianța este după cum urmează:
Găsim probabilitatea unei valori a unei variabile aleatoare care are o distribuție uniformă pe intervalul care aparține în întregime intervalul [a. b]:
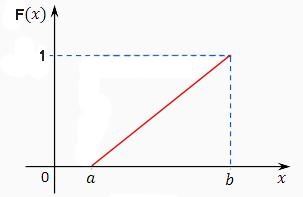
Funcția de distribuție ia forma:
Trenurile de metrou circulă în mod regulat, la intervale de 2 minute. Pasagerul intră platforma la un moment aleatoriu. Care este probabilitatea ca un pasager va trebui să aștepte mai mult de o jumătate de minut.
Găsiți media și deviația standard a unei variabile aleatoare X - timpul de așteptare a trenului.
Aleatoare X variabilă - un tren timp de așteptare pe timpul (în minute) a intervalului [0, 2] are o uniformă a legii de distribuție f (x) = 1/2.
Prin urmare, probabilitatea ca un pasager va trebui să aștepte mai mult de o jumătate de minut este egal cu 1/4 din suprafața unui dreptunghi este egal cu unitatea, adică,
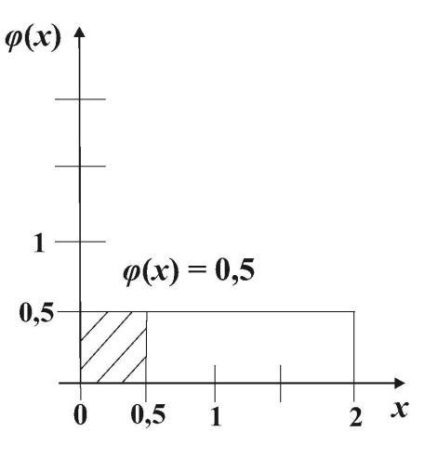
Ne găsim așteptarea și variația abaterii standard:
12. Chance predeterminate variație. de regulă cu trei sigma.
Teorema. Abaterea modul Probabilitatea unei variabile aleatoare X continuă de la așteptarea matematică a valorii unui număr arbitrar de mic ε> 0 este dată de:
(*)
Regula trei sigma.
Substituind valoarea ε în (*), obținem:
Deci, cu o probabilitate în mod arbitrar aproape de unitate se poate argumenta că abaterea unitară a unei variabile aleatoare distribuite în mod normal, din valoarea sa de așteptat să nu depășească de trei ori abaterea standard.
Teorema limită centrală.
Teorema limită centrală este teoria grupurilor dedicate stabilirii condițiilor în care există o distribuție normală. Printre aceste teoreme un loc important aparține teorema lui Lyapunov.
Dacă variabila aleatoare X este suma unui număr mare de reciproc - variabile aleatoare independente, adică, efectul fiecăreia dintre care întreaga cantitate este neglijabilă, atunci variabilele aleatoare are o distribuție se apropie la infinit distribuția normală.
Momentele inițiale și centrale ale continuă aleatoare variabilă, și aplatizării. Skewness Modul și mediana.
În probleme aplicate, cum ar fi tistike o sută de matematică, studiul teoretic al empirice de distribuție-diviziuni, diferită de distribuția normală, OMS-apare necesitatea unor estimări cantitative ale acestor diferențe. În acest scop, am introdus caracteristici speciale adimensionale.
Opredelenie.Moda continuu variabilă aleatoare (Mo (X)) - este valoarea cel mai probabil, pentru care probabilitatea pi sau densitate de probabilitate f (x) atinge un maxim.
Opredelenie.Mediana velichinyX aleatoare continuă (Me (X)) - aceasta este valoarea sa, care satisface ecuația:
P (X
Geometric, o linie verticală x = Me (X) împarte aria de sub curba forma în două părți egale.
La punctul X = Me (X), funcția de distribuție F (Me (X)) =
Găsiți modul Mo, mediana Me și așteptarea matematică M a unei variabila aleatoare X cu f densitate de probabilitate (x) = 3x 2. când x Î [0; 1].
Densitatea de probabilitate f (x) este maxim la x = 1, adică f (1) = 3, prin urmare, Mo (X) = 1 intervalul [0; 1].
Pentru a găsi mediana denota Me (X) = b.
Deoarece Me (X) satisface condiția P (X apoi P (-∞ Nota 3 valoarea rezultată Mo (x), Me (X), M (X) pe axa Ox: distribuția teoretică Opredelenie.Asimmetriey este raportul dintre treilea moment central, pentru un minut la cubul abaterii standard: distribuția teoretică Opredelenie.Ekstsessom se numește pe valoarea determinată prin ecuația: în cazul în care - punctul central al patrulea ordin. Pentru o distribuție normală. Atunci când abaterea, în afară de asimetria distribuție normală pozitivă în cazul în care „lung“ și partea flata a curbei de distribuție este la dreapta punctului în modul corespunzător abscisa-conductoare; în cazul în care această parte a curbei din stânga a modei, asimetria este negativ (Fig. 1a, b).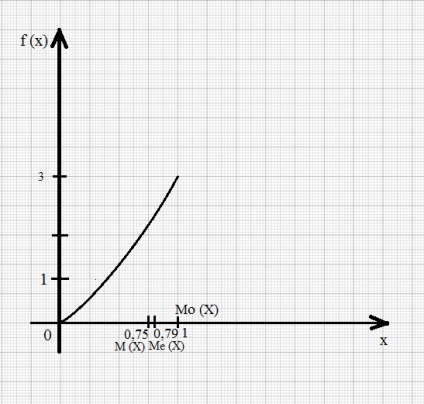

Kurtosis caracterizează „prăvăliș“ al creșterii curbei, distribuția fisiune în comparație cu curba normală dacă aplatizare polo-rezidenți, curba are un vârf înalt și ascuțit; în cazul curbei aplatizării negativ pentru a se potrivi și are un top înclinat, inferior.
Se va aprecia că, prin utilizarea comparației menționate caracteristicile de referință sunt ipoteze similare cu privire la valorile de așteptare matematice și dez-persia pentru distribuții normale și teoretice.
Exemplu. Lăsați un discret X variabila aleatoare este dată legea de distribuție:
Găsiți: skewness și kurtosis a distribuției teoretice.
Ne găsim mai întâi așteptarea variabilei SLE-aleatoare:
Apoi vom calcula inițiale și centrale momentele 2, 3 și ordinea 4-lea și deviația standard:
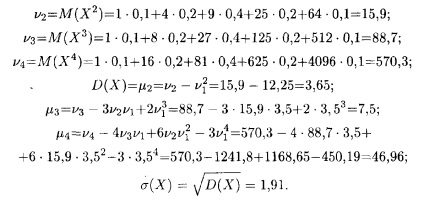
Acum găsim formule pentru plumb-clasele necesare:
În acest caz, „lungimea“ a curbei de distribuție a unei curse-a pus la dreapta moda, curba in sine nu-mult mai mult decât a atins punctul culminant curba normală cu aceleași valori ale speranța matematică și varianța.
Teorema. Pentru un X variabilă aleatoare arbitrare, precum și orice număr
Ԑ> 0 inegalitățile:
- probabilitatea de inegalitatea opusă.
Să X -Expenses apă pe animal de fermă (n).
Prin ipoteză, M (X) = 1000.
Aceasta nu este mai mică de 0,96.
Pentru binomială inegalitatea Cebîșev de distribuție ia forma: