Proprietățile de rădăcini pătrate.
- ;
- dacă ≥ 0 și b> 0;
- dacă ≥ 0 și n - un număr întreg;
- dacă ≥ 0 și n - număr natural.
- Notă (5) 2 = 25, dar.
- Rădăcina nu poate fi egal cu numărul de non-pozitive.
- - este imposibil să se calculeze rădăcina pătrată a unui număr negativ nu există.
- Dacă, atunci b 2 = a. când a ≥ 0 și b ≥ 0. este una dintre cele mai importante proprietăți ale rădăcinilor.
- Este important să se înțeleagă că rădăcina pătrată - este un alt nivel de intrare ½:
- Valoarea rădăcină nu se schimba în cazul în care o creștere a ratei de a n ori și, în același timp, a construi o valoare rădăcină pătrată a puterii de n:
- Valoarea rădăcină nu se schimbă dacă exponentul este redus de n ori și în același timp, se extrage rădăcina de gradul n-lea a valorilor rădăcinii pătrate:
- Rădăcina câtul este egal cu raportul dintre rădăcina pătrată a dividendului prin rădăcina divizorul de (indicatori rădăcini ar trebui să fie aceleași):
- Pentru a construi rădăcină în gradul suficient pentru a construi acest nivel al valorii rădăcină pătrată:
Pe de altă parte, pentru a elimina rădăcina în măsura să ridice suficient în acest grad rădăcină de la nivelul solului:
- Rădăcina produsul mai multor factori, este egală cu produsul dintre rădăcinile același grad de acești factori (de asemenea, o proprietate importantă a rădăcinilor):
In schimb, produsul din rădăcinile același grad egal cu aceeași rădăcină a produsului de valori ale radicalilor:
Rădăcina pătrată ca o funcție elementară.
rădăcină pătrată - este o funcție elementară și un caz special al unei funcții de putere cu. Aritmetică rădăcină pătrată este netedă când, iar la zero este continuu pe dreapta, dar nu diferențiată (rădăcini svoytvo distins).
Ca o funcție de rădăcină variabilă complexă - o funcție cu două valori, care listează converg spre zero.
Proprietatea în funcție de rădăcină.
La [0; + ∞) pot fi furnizate pentru fiecare număr x conform rădăcinii Singular de gradul n-x pentru orice valoare a lui n.
Adică, aceasta înseamnă că pe platoul de filmare [0; + ∞) putem vorbi de funcția rădăcină:
Acum definim proprietățile funcției de rădăcină și se construiește graficul acesteia.
Principalele proprietăți ale rădăcinii ca funcție de:
Intervalul [0; + ∞) - un domeniu.
Deoarece număr non-negativ este rădăcina n grade de număr non-negativ, atunci intervalul [0; + ∞) este domeniul valorilor funcției.
Deoarece setul simetric nu este domeniul funcției, astfel încât funcția nu este nici ciudat, nici măcar.
Operația de extragere a rădăcinii a fost administrată ca o operație inversă ridicării la un nivel adecvat.
Deci, se poate argumenta că:
Acum puteți complot funcția rădăcină.
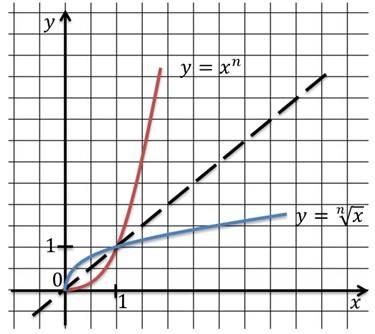
Folosind grafic, putem scrie proprietățile rămase ale funcției.
In intervalul [0; + ∞) crește funcției.
Funcția Top nu este limitată, dar este limitată de mai jos, de exemplu, o linie dreaptă de la care = -0.5.
Întregul domeniu al funcției este convexă în sus.
Am caracteristica cea mai mică valoare va fi 0, iar cea mai mare valoare are.
Dacă fiecare dintre punctele de unele funcții interval este diferențiabilă, aceasta înseamnă că o anumită perioadă este continuă.
În orice moment în intervalul [0; + ∞) există, acest derivat, singura excepție este punctul 0.
Deoarece în orice punct din intervalul (0; + ∞) funcția are un derivat, aceasta înseamnă pe intervalul, funcția (0 + ∞) este diferențiabilă.