Suprafața unei figuri plane
Am observat deja expresia aria trapezului curbilinie prin definit integralei. Rezultă formula de calcul aria figurii delimitate de sus și de jos a graficului funcției. și pe părțile laterale și drepte:
Dacă trapezului curbiliniu delimitată mai sus de linia definită de ecuațiile parametrice: ,,. zona a figurii se calculează după cum urmează
în care limitele de aliniere se efectuează în conformitate cu valorile :.
Exemplu. Se calculează aria figurii delimitată de o elipsă :.
Luați în considerare jumătate cifra situată în jumătatea superioară. De la stânga la dreapta sunt coordonatele valorilor limită și numărul. în conformitate cu acestea definesc limitele de integrare pentru parametrul de relațiile: și. Prin formula descoperire
în cazul în care pentru zona situată în interiorul elipsei obținem formula.
Ca un exercițiu, se recomandă să se obțină o formulă pentru calcularea suprafeței figurii date în coordonate polare. limite sunt razele. și curba
Lungimea arcului curbei
Lăsați arcul curbei reprezintă graficul funcției care este continuă în intervalul. Lungimea arcului acestei curbe este definită ca limita la care tinde lungimea inscripționată polyline (vezi. Fig. 2) și când.
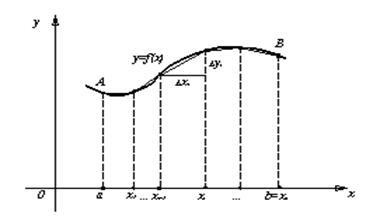
Această definiție corespunde lungimii arcului unei intuitii curbe și este baza conceptului strict lungime logică.
La setarea ecuațiile parametrice ale curbei, ale ecuației (12) se obține prin formula
Reglarea arcului ecuației curbei în coordonate polare. Acesta este un caz special de sarcini parametrice :. După substituirea acestor funcții se obține o formulă pentru lungimea arcului curbei, dată în coordonate polare,
Exemplu. Se calculează lungimea arcului primelor arce cicloidale (traiectorii ale jantei roții) prezentate în Fig. 3.
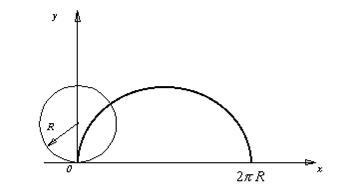
Cicloidale are o ecuație parametric. Parametrul este unghiul de rotație al roții, care, pentru primul arc ia valori. Conform (13) lungimea arcului este exprimat prin integrala cicloida
Volumul și suprafața Suprafața corpului revoluției
Noi pune problema determinării volumului și suprafeței corpului zonei, curba obținută prin rotirea unui arc în jurul axei.
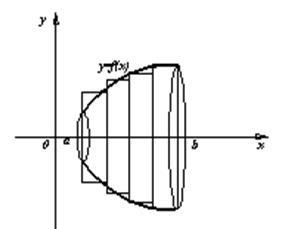
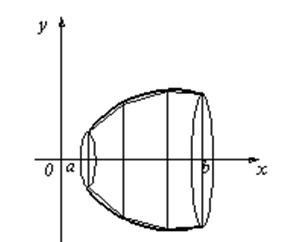
Capacitatea este definită ca valoarea limită a volumului corpului cilindric compozit prezentat în Fig. 4. Suprafața corpului de rotație se obține în limita suprafeței compozit inscripționată suprafețe conice (vezi. Fig. 5).
Ca rezultat, am ajuns la formulele de calcul al zonei de volum și de suprafață:
Vă rugăm să rețineți că utilizarea unui corp cilindric compozit nu dă valoarea corectă a suprafeței.