Compararea primului grad cu o singură necunoscută este:
Rezolva comparație - înseamnă a găsi toate valorile lui x-l satisface. Două comparații, care sunt satisfăcute de aceleași valori ale lui x sunt numite echivalente.
În cazul în care comparația (1) satisface orice x = x1, apoi (în funcție de 49), comparativ cu aceeași și va satisface toate numerele comparabile cu x1. modulo m. x x1 (mod m). Această întreagă clasă de numere este considerat ca o soluție. În cazul în care un astfel de acord poate concluziona că.
66.Sravnenie (1) va avea cât mai multe soluții ca reziduurile sistemului complet i se potrivește.
6x - 4 0 (mod 8)
printre numerele 0, 1,2, 3, 4, 5, 6, 7 sistem complet de reziduuri modulo 8 satisfac două numere: x = 2 și x = 6. Prin urmare, comparația de mai sus are două soluții:
x 2 (mod 8), x 6 (mod 8).
Compararea primul grad de transfer liber al membrului (cu semnul opus), în partea dreaptă a formularului
Luați în considerare comparația satisface condiția (a. M) = 1.
66 Conform comparația noastră are cât mai multe soluții ca reziduurile sistemului complet i se potrivește. Dar când x se execută printr-un sistem complet de reziduuri modulo m, atunci ax ruleaza printr-un sistem complet de resturi (60). În consecință, atunci când unul și numai o singură valoare a lui x, care este luat dintr-un sistem complet va fi comparabil cu ah b. Astfel,
67. (a, m) = axb 1 comparație (mod m) are o soluție.
Acum sa (a. M) = d> 1. Apoi, comparația (2) are o soluție, este necesar (55) până la b împărțit la d, altfel comparația (2) este imposibil pentru orice x general. Presupunând totuși multiple b d, setați o = a1d. b = B1d. m = m1d. Apoi, o comparație (2) este echivalentă cu următoarele valori (prin reducerea la d): a1xb1 (mod m), care deja (A1 m1.) = 1 și, prin urmare, acesta va avea o singură soluție modulo m1. Fie X1 - cel mai mic reziduu nenegativ din această soluție modulo m1, atunci toate numerele x, formând soluția, există o
Modulo este mchisla (3) formează mai mult de o soluție și mai exact cât mai multor soluții numerele (3), există un număr de 0, 1, 2 ,. m - 1 a reziduurilor mici nonnegative modulo m. Dar aici se vor obține următoarele numere (3):
și anume d total de numere (3); prin urmare, comparația (2) are o d luare.
68. Fie (a, m) = d. Comparație ax b (mod m) este imposibilă, în cazul în care b nu este divizibil cu d. Când b, un multiplu de d, d este soluțiile de comparație ..
Soluții 69.Sposob care compară primul grad, bazat pe teoria fracțiilor a continuat:
Extinderea raport fracțiune a continuat m: a,
și luând în considerare ultimele două convergents:
în funcție de proprietățile fracțiunilor continue (conform 30), avem
Astfel, comparația are o soluție
pentru constatare, care este suficient pentru a calcula Pn- 1 conform cu procedura descrisă pentru 30.
Exemplu. Rezolvam comparație
111x = 75 (mod 321). (4)
Aici (111, 321) = 3, și 75, un multiplu de 3. Prin urmare, comparația are trei soluții.
Impartind ambele părți și compararea unității 3, obținem o comparație
37x = 25 (mod 107) (5)
că ar trebui să rezolve mai întâi. avem
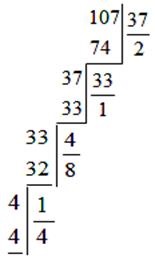
Prin urmare, în acest caz, n = 4, Pn-1 = 26, b = 25, avem o soluție și compararea (5) sub forma
x -26 # 8729; 25 99 (mod 107).
Din această comparație, (4), deciziile sunt prezentate după cum urmează:
x 99; 99 + 107; 99 + 2 # 8729; 107 (mod 321),
x º99; 206; 313 (mod 321).
Calcularea elementului invers al unui anumit modul
70.Esli numere întregi a și n sunt relativ prim, există o“. satisfăcătoare decât o # 8729; o „≡ 1 (mod n). Numărul de „numit inversul multiplicativ modulo n și o denumire utilizate pentru ea - 1 (mod n).
Calculul valorilor inverse ale unor module pot fi realizate comparând gradul întâi cu o singură soluție necunoscută, în care numărul de „este luat ca x.
Pentru a găsi o soluție de congruența
Puteți utiliza algoritmul lui Euclid (69) sau teorema lui Fermat, Euler, care prevede că, în cazul (a, m) = 1, atunci
Grupurile și proprietățile lor
Grupul - una din clasele taxonomice utilizate în clasificarea structurilor matematice cu proprietăți caracteristice comune. Grupurile au două componente: un set (G) și exploatare () definite pe acest set.
Conceptele de seturi, elemente și accesorii sunt concepte nedefinite de bază ale matematicii moderne. Orice set de elemente este determinată, care îi aparțin (care, la rândul lor, pot fi, de asemenea, seturi). Astfel, spunem că setul este definit sau set, dacă putem spune dacă este sau nu acest set aparține oricărui element.
Pentru două seturi A, B înregistrare BA. BA. B ∩ A. BA. B \ A. A × B, reprezintă, respectiv, B este un subset al A (adică orice element al lui B este conținută și în A. de exemplu, mulțimea numerelor naturale conținute în setul de numere reale, în plus, întotdeauna AA), B este un subset adecvat al setului a (adică, BA și B ≠ a), intersecția seturilor B și (adică toate elementele care stau atât în A. și B. de exemplu, numere întregi de intersecție și numere reale pozitive este multimea numerelor naturale), unirea seturilor B și a (adică setul format din elementele Care se află fie în sau A. B), diferența seturi B și A (adică, o multitudine de elemente care se află în B. dar nu se află în A), produs cartezian de mulțimi A și B (adică, o multitudine de perechi specii (a. b), unde aA. bB). Prin | A | a indicat întotdeauna că cardinalitatea A. numărul de elemente din setul A.
Operațiunea - o regulă conform căreia oricare două elemente ale setului G (a și b) îi este atribuit un al treilea element al G: și b.
Multitudinea de elemente cu o operație numită bandă G. în cazul în care sunt îndeplinite următoarele condiții:
1. asociativitatea. pentru toate elementele a, b, cG egalitatea a (b c) = (a b) c.
2. Unitatea de celulă: există un element e G, că pentru orice G Equalities un e = e a = a.
3. Element Reverse. fiecare G există există un element de 'G. satisfăcând relația unui' = a „= a e.
Un element e al lui G numit elementul neutru al grupului și elementul a „- elementul invers pentru. Elementul de întoarcere este notată o „= a - 1.
Grupuri de operare comutative. care este, pentru orice pereche o. b G egalitatea a b = b a. numitele grupuri comutative, sau grupuri abeliene.
Numărul de elemente din grup se numește comanda acestuia.
În ceea ce privește rezolvarea ecuațiilor proprietatea de bază a grupului este că acesta a permis în mod clar tipul de ecuație:
pentru orice a, b G.
1.,,, numere întregi raționale reale complexe sub plus.
2. nenule raționale, numere complexe, reale sub multiplicare.
Toate aceste grupuri sunt abeliene.