Fluxul câmpului electric. Teorema lui Gauss în formă integrală
4. Divergența câmpului vectorial. Teorema lui Gauss în formă diferențială,
câmp vectorial arbitrara (adică, o funcție de vector. In puncte prestabilite (x, y, z) dintr-o regiune a spațiului) pot fi asociate scalar funcție numită câmp de divergență F. Această funcție este notată cu «div» și este determinată de relația
Sensul fizic de divergență din formulă este dovedită în cursul matematici superioare:
Dacă valoarea limită a V S și concentrația sa de suprafață este în punctul de observație, în care divergența calculată. Conform (1.4.1), fluxul de tensiune E prin orice sferă infinitezimal mică, în care nici taxe - identic zero. Prin urmare, (1.4.2), rezultă că punctele cu densitate zero, încărcare (r = 0) E divergență dispare. După analizarea fluxului prin sfera mică în jurul punctului V, în care divergența tensiunea nu zero, poate fi demonstrat prin utilizarea (1.4.1) și (1.4.2). că, la un moment dat în sarcină spațială este, prin urmare, punctul în care tensiunea de divergență diferite de zero, sunt surse de linii electrice.
Cursul matematică dovedesc o teorema Gauss-Ostrogradskii (a fost stabilită de Gauss în 1844, indiferent de MV Ostrogradskii sa dovedit a fi în 1839):
Aici V - volumul arbitrar suprafața delimitată S. aplică Teorema (1.4.3) la fluxul câmpului electrostatic. În ceea ce privește (1.4.1), obținem:
Din egalitatea integralelor este volumul arbitrar V datorită egalității integrands, adică Teorema lui Gauss', în formă diferențială (A. Poisson 1850 YG):
Dintre acele regiuni ale spațiului unde E divergență este pozitiv, liniile de câmp emane E (r> 0), în acele zone în care Scufundă- <0 силовые линии заканчиваются (r<0), а через те области, где divE = 0 силовые линии проходят, но не рождаются и не исчезают, так как в этих областях r=0 (зарядов нет).
Rotorul circulație și câmpul vectorial. Gradientul unei funcții scalare
Circulation CL câmp vectorial arbitrar F (x, y, z) este definită prin următoarea relație într-un circuit închis L:
în care Fl - proiecția vectorului pe direcția F element de circuit dl (vezi Figura 1.5.1 ..).
Rotorul - acesta este un alt concept din teoria matematică a câmpurilor vectoriale. Într-un sistem de coordonate cartezian (x, y, z) rotor F (denumirea «ROTF») este definit ca un vector ale cărui componente sunt anumite combinații ale derivaților spațiale ale vectorului F, și anume:
Rotor sensul fizic rezultă din ecuație, se dovedește în cursul matematică:
În cazul în care n - normală la sol S, L - contur care delimitează situl, care în acest caz este contractat limita la punctul de observație. Dacă vectorul câmp rotor la un punct de observație nu este egal cu zero, atunci orice vecinătate suficient de mică de puncte liniilor de câmp formează buclă închisă microscopice în jurul ei ( „swirl“). Prin urmare, regiunea în care rotorul câmp vectorial este diferit de zero, se numește câmpul turbionar și câmpul însuși, al cărui rotor este diferit de zero numit vortex. Viteza fluxului de lichid sau gaz, considerată ca o funcție a coordonatelor, este un exemplu clar al unui câmp vectorial. Turbulența în lichid sau gaz se formează în jurul punctelor în care rotorul este rata nenulă debitului de fluid (gaz). Câmpul de imagine prin intermediul liniilor electrice în spațiul în care rotorul este diferit de zero (în același mod ca și în punctele cu nenulă divergență), este imposibil.
După cum se va vedea mai târziu, circulația și rotorul câmpurilor electrostatice sunt identic zero, în întregul spațiu. Prin urmare, câmpul electrostatic - câmp de forță este relativ simplu. Aceste aceleași proprietăți și câmpul gravitațional.
Conceptul gradientului este deja introdus în cursul mecanicii. Rechemare-l. Gradientul f (x, y, z), depinde de coordonatele - este un vector ale cărui componente sunt carteziene derivatele spațiale ale funcției f:
Să. Putem arăta că, dacă este necesar și suficient ca rotorul este zero:
Potențialitatea câmpului electrostatic. potențial electric
Munca de teren pe un transfer de sarcină q test de la un punct de la 1 la un punct 2 nu depinde de traiectoria mișcării sale și este definit pentru teren și taxa de numai coordonatele acestor puncte. Pentru cazul în care câmpul sursă este o sarcină Q punct (Fig. 1.6.1), acest lucru poate fi ușor justificată după cum urmează. De lucru pe un segment elementar al traiectoriei, binecunoscuta definiție a mecanicii, și anume :. Extinderea produsului scalar al vectorilor printr-un unghi a între ele, obținem
In plus fata (de integrare) toate lucrările elementare, vom găsi
QED. Munca este definită doar de distanțele de la sursa la punctele inițiale și finale ale traiectoriei. Un astfel de câmp de forță în mecanică am numit potențial.
Din principiul superpoziției trebuie potențialitate camp electrostatic creat de taxele oricărui sistem. De la (1.6.2) și principiul superpoziției, de asemenea, implică faptul că activitatea forțelor electrostatice de pe taxa este transportat într-un circuit închis este egal cu 0:
Astfel, pentru fiecare circuit în circulație a intensității câmpului electrostatic - identic zero. În conformitate cu afirmația (1.5.6) a intensității câmpului electrostatic (până la un semn), acesta poate fi interpretat ca un gradient al unei funcții de coordonate, numite potențiale câmpuri electrostatice:
Folosind definiția intensității câmpului electrostatic (1.2.1) și legătura dintre formula forță F și potențial W de energie, cunoscute din mecanica desigur
din (1.6.4), care câmpul potențial, la un moment dat de observație este numeric egală cu energia potențială a unui sarcină q încercare, plasate în punctul dat, împărțit la amploarea acestei taxe:
Energia potențială a câmpului electrostatic ca energia intensității câmpului gravitațional este definit până la o constantă arbitrară, care poate fi fixat pentru acest punct zero la W. În general, energia potențială a unui câmp electrostatic este egală cu zero la infinit.
Formula (1.6.4), prin integrarea cu ușurință obține o formulă referitoare la potențialul de intensitate:
Integrarea în (1.6.7) poate fi realizată prin orice curbă care leagă punctele 1 și 2.
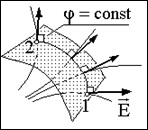
În spațiul unde există un câmp electrostatic, o suprafață mentală perpendiculară pe liniile de câmp. La calcularea integrală (1.6.7), 1-2 de-a lungul oricărei traiectorie, situată pe suprafața, componenta tangențială Et E este zero. Prin urmare, pentru oricare două puncte 1 și 2 din suprafața laterală dreapta (1.6.7) este zero, potențialele j (r1) și j (r2) sunt egale. Suprafața, în toate punctele în care potențialul are aceeași valoare, numită echipotențiale. Astfel, suprafața este perpendiculară pe liniile de câmp echipotențiale.
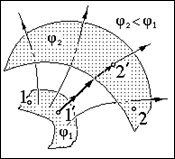
În general, diferența de potențial între punctele 1 și 2 este egală cu diferența de potențial dintre suprafețele echipotențiale, care aparțin aceste puncte. Acestea din urmă pot fi găsite prin efectuarea integrării în ecuația (1.6.7) pe liniile electrice care leagă punctele 1 și 2 ¢ ¢ aceste suprafețe echipotențiale. Atunci când acest lucru este de fapt integrantă modulul E al câmpului electric, deoarece pe linia de alimentare. In concluzie, pentru o taxă punct Q potențial câmp vom da o formulă care rezultă din compararea formulelor (1.6.2) și (1.6.6) și rata cunoscută de funcționare a mecanicii relației dintre potențialii A12 forțe pe porțiunea traiectoriei particulei 1-2 și energia potențială a particulelor în începând W1 și W2, la sfârșitul acestei secțiuni:
În acest caz, particula este un test de sarcină q. Formula pentru un potențial punct îndepărtat de la un Q punct sursă la distanța r. arată
Câmpul electric - o formă particulară domeniu care există în jurul organelor sau particule care au o sarcină electrică, precum și în formă liberă în undele electromagnetice. Câmpul electric este direct vizibil, dar poate fi observată prin acțiunea sa și cu ajutorul instrumentelor. Acțiunea principală a câmpului electric este accelerația corpurilor sau particule având o sarcină electrică.
Câmpul electric poate fi privit ca un model matematic care descrie valoarea câmpului electric la un moment dat în spațiu. DUGLAS Dzhankoli a scris: „Trebuie subliniat faptul că domeniul nu este un fel de substanță, ci mai degrabă, este un concept extrem de util ... Problema“ realității „și existența câmpului electric, de fapt - este o întrebare filosofică, într-adevăr metafizic în înțelegerea fizica. câmp sa dovedit a fi extrem de util - este una dintre cele mai mari realizări ale minții umane ".
Câmpul electric este o componentă a câmpului electromagnetic și o singură manifestare a interacțiunii electromagnetice.
Referințe
Fluxul câmpului electric. Teorema lui Gauss în formă integrală
Informații despre „câmpul electric“
Categorie: Fizică
Numărul de caractere, inclusiv spații: 24053
Număr de mese: 1
Numărul de imagini: 7
curent pe două variabile: polarizarea și viteza potențială schimbare. Această abordare permite modelarea câmpurilor electrice tranzitorii în sistemele electrochimice. Modelul matematic este considerat umplut cu conductor regiune D mediu, unde S delimitare este format din anod SA, catod Sk și Si izolat site-uri: S = Sa # 61525; Sc # 61525; Si, = D # 61525; S, dependența.
de două ori. Experiența arată că forța de interacțiune este redus la jumătate. Reiterând o tehnică similară, vă puteți asigura că puterea este proporțională cu produsul taxelor. Deoarece câmpul electric este interacțiunea a două taxe? Inițial a crezut că taxele direct peste actul anulat reciproc. Fiecare taxa de la o distanță „se simte“ prezența celuilalt. A fost atât.
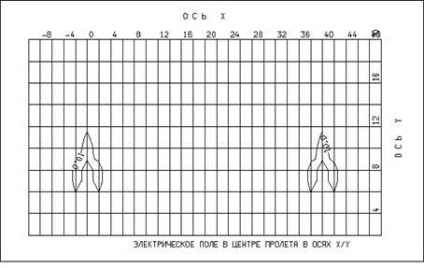
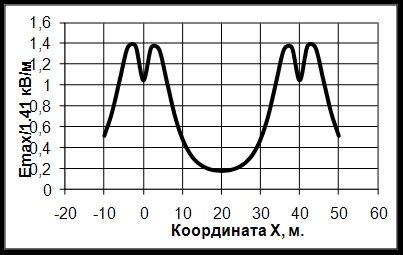
punerea sa în aplicare. 1. câmpuri electrice prezente la rationalizarea de nivel internațional și într-un număr de țări dezvoltate, inclusiv propriile noastre, dezvoltate și documentele care reglementează nivelurile câmpurilor electrice generate de echipamente de înaltă tensiune și aprobate. Primele norme privind câmpurile electromagnetice au fost stabilite în [1, 2, 3, 4, 5]. În România, sunt reglementate.
participarea ionilor negativi în procesul de oxidare lentă. Rezumând toate cele de mai sus, trebuie remarcat faptul că cele două puncte principale de vedere cu privire la mecanismul de acțiune a câmpului electric asupra procesului de ardere (influență asupra dinamicii gazelor a procesului sau un impact direct asupra cineticii de reacție) este o reflectare a celor două mai multe concepte generale în ceea ce privește rolul și locul de particule încărcate în procesul de ardere, unul.