.
15.1.4. Divergența câmpului vectorial
Caracteristici Integral - flux și liniar integrantă - caracterizarea câmpului vectorial „ca un întreg“. O caracteristică cantitativă a câmpului pentru a da fiecare punct, prezentat mai jos, caracteristici diferențiale. Noi introducem conceptul de divergență.
Inconjoara suprafață punctul M arbitrar (S) de formă arbitrară (de exemplu, sferă suficient de rază mică). Fie (V) - volumul conținut în suprafața (S).
Definiția. Limita de capăt a raportului câmpului de curgere prin suprafața (S) a volumului inclus în acesta, la contracția suprafeței la punctul M și aspirație volum V la zero se numește divergența câmpului vectorial la punctul M:
Notă. Definiție (1.10) este invariantă (independent de sistemul de coordonate) definirea divergență.
Divergențele caracterizează pe câmp vectorial debit unitate de volum, „outgoing“ M. adică putere punctul sursă (la) sau de scurgere (at) la punctul M.
Într-un sistem de coordonate cartezian divergență se calculează cu formula:
Proprietăți divergență. Să - Vector Domenii - funcția scalară. apoi:
Având în vedere formula (1.10) rescrierea Gauss (1.6)
- flux câmp vectorial printr-o suprafață (S) închisă este egal cu volumul triplu integral (V), găzduit în interiorul suprafeței divergența câmpului.
Exemplul 1. Se calculează.
Exemplul 2. Se calculează unde u (M) - funcția scalară, - o funcție vectorială.
Decizie. Formula (1.10) vom găsi.
Exemplul 3. Folosind teorema Gauss (1.12), găsiți câmpul vectorial de curgere prin întreaga suprafață (S) a corpului (V):
în direcția normala exterioară.
Decizie. Avem. Prin urmare, =. Pentru a calcula triplu integralei trece la coordonate cilindrice. Ecuația suprafeței ia formează =.
15.1.5. Rotor câmp vectorial (vortex)
Să presupunem că câmpul - câmp diferențiabilă (adică proiecția câmpului vectorial pe axele de coordonate sunt funcții derivabile).
Definiția. câmp vectorial turbionară (putregaiul notat) este un vector al cărui proiecție pe un vector arbitrar este determinat ca limita domeniul relației de circulație în ceea ce privește unele circuite (L), care cuprinde punctul M. și situată într-un plan perpendicular pe vectorul, în zona regiunii delimitate de acel contur, cu condiția că bucla este contractată la punctul zona M. și zona (S) tinde la zero:
În spațiul tridimensional prin coordonate rectangulare carteziene ale unui vector este exprimat după cum urmează:
sau convenabil pentru stocarea formă simbolică
Stokes teorema. Lăsați coordonatele vectorului + continuu și au derivaților continue. Apoi circulația câmpului vectorial pe un circuit închis (L) este egal cu câmpul de curgere printr-o suprafață arbitrară vortex (S), calibrat prin bucla:
Se presupune că orientarea contur (L) și suprafața (S) a convenit: calea circuitului pozitiv este direcționat de la normal „toe-to-head“.
proprietăți ale rotorului: 1); 2).
Definiția. câmp vectorial Irrotational se numește în arta (V), în cazul în care.
Exemplul 1: găsi vectorul câmp magnetic câmp rotor.
Reshenie.Vektor sub formă de coordonate:
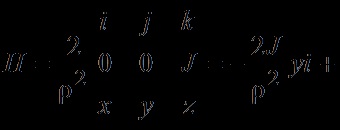
+ -
- intensității câmpului - câmp irrotational.
Exemplul 2. Se calculează vectorul circuitului de circulare 1) în mod direct, 2) conform teorema lui Stokes.