Lucrul prin mutarea corpului într-un câmp de forță;
Câmpul magnetic în jurul unui conductor cu un curent (Legea lui Ampere);
inducție electromagnetică într-o buclă închisă cu fluxul magnetic (Legea lui Faraday).
Considerăm că acestea mai detaliat cu exemple de aplicații.
Să presupunem că o bucată de sârmă descrie o curbă \ spațială (C. \) Să masa este distribuită de-a lungul acestei curbe la o densitate \ (\ rho \ stânga (\ dreapta). \) Apoi, greutatea totală a curbei este exprimată printr-o integrală linie a primului tip \ [m = \ int \ limits_C \ dreapta) ds>. \] Dacă curba \ (C \) este definit într-o formă parametric utilizând o funcție vector \ (\ mathbf \ stânga (t \ dreapta) = \ stânga (\ dreapta), \) atunci ei descrisă în masă de \ [m = \ dreapta) \ sqrt >>> \ dreapta)> ^ 2> + >>> \ dreapta)> ^ 2> + >>> \ dreapta)> ^ 2 >> dt>.> \ ] în cazul unei curbe plan definit de un plan \ (Oxy, \) este definită ca masa de \ [m = \ int \ limits_C \ dreapta) ds> \] sau parametrically formă th \ [m = \ dreapta) \ sqrt >>> \ dreapta)> ^ 2> + >>> \ dreapta)> ^ 2 >> dt>.> \]
Centrul de masă și momentele de inerție ale curbei
Din nou, lasa o bucată de sârmă descrie o curbă \ (C \) și distribuția masei de-a lungul curbei definită densitate funcție continuă \ (\ rho \ left (\ dreapta). \) Apoi, coordonatele centrului a formulelor definite mase de curba \ [\ bar x = \ frac >>>, \; \; \ bar y = \ frac >>> \; \; \ bar z = \ frac >>> \] unde \ [> = \ int \ limits_C \ dreapta ds)>,> \; \;> = \ int \ limits_C \ dreapta) ds>,> \; \;> = \ int \ limits_C \ dreapta) DS >> \] - așa-numitele momente de prim ordin.
Momentele de inerție în jurul axelor \ (Ox, Oy \) și \ (Oz \) sunt definite \ [= \ int \ limits_C +> \ dreapta) \ rho \ left (\ dreapta) ds>,> \; \; = \ Int \ limits_C +> \ dreapta) \ rho \ left (\ dreapta) ds>,> \; \; = \ Int \ limits_C +> \ dreapta) \ rho \ left (\ dreapta) ds>.> \]
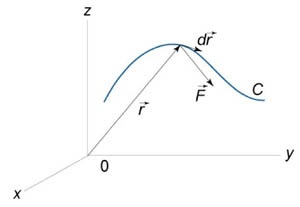
Munca prin deplasarea corpului într-un câmp de forță \ (\ mathbf \) de-a lungul curbei \ (C \) este exprimat printr-o integrală linie al doilea tip \ [W = \ int \ limits_C \ cdot d \ mathbf> \] unde \ (\ mathbf \) - forța care acționează asupra corpului, \ (d \ mathbf \) - versorul tangentei (Figura \ (1 \)). Simbolul \ (\ cdot d \ mathbf> \) reprezintă produsul scalar al vectorilor \ (\ mathbf \) și \ (d \ mathbf. \)
Rețineți că câmp de forță \ (\ mathbf \) nu este în mod necesar cauza mișcărilor corpului. Organismul se poate deplasa sub influența altor forțe. Într-un astfel de caz, forța de muncă \ (\ mathbf \) poate fi uneori negativ.
Dacă câmpul vectorial este setat în formă de coordonate într-un \ [\ mathbf = \ stânga (\ dreapta), Q \ stânga (\ dreapta), R \ stânga (\ dreapta)> \ dreapta) \] munca de teren se calculează cu formula: \ [W = \ int \ limits_C \ cdot d \ mathbf> = \ int \ limits_C. \] în cazul particular atunci când corpul se mișcă de-a lungul unei curbe plat \ (C \), în planul \ (Oxy, \), formula \ [W = \ int \ limits_C \ cdot d \ mathbf> = \ int \ limits_C, \] unde \ (dreapta), Q \ stângă \ mathbf = \ stânga (\ (\ dreapta)> \ dreapta). \)În cazul în care câmpul vectorial \ (\ mathbf \) potențial. funcționarea mișcării a corpului din punctul \ (A \) la punctul \ (B \) este exprimat prin \ [W = u \ din stânga (B \ dreapta) - u \ stânga (A \ dreapta) \] unde \ (u \ stânga (\ dreapta) \) - potențialul terenului.
Greutatea corporală \ (m \) este turnat într-un unghi la orizont \ (\ alpha \) la o rată inițială \ (\) (Figura \ (6 \)). Calculați forța de muncă de atracție \ (\ mathbf = m \ mathbf \) în timpul deplasării corpului până la momentul impactului cu solul.
Scriem legea de mișcare a unui corp într-o formă parametrică. \ [X => t = \ cos \ alpha \ cdot t \] \ [y => t - \ frac >> = \ păcat \ alpha \ cdot t -. \ Frac >> \] La coliziune cu solul \ ( y = 0, \), astfel încât timpul de zbor al corpului este egal \ [\ păcatul \ alpha \ cdot t - \ frac >> = 0> \; \; \ Sin \ alpha - \ frac >> \ dreapta) = 0,> \; \; \ Sin \ alpha >>.> \] Forța gravitațională poate fi scrisă ca \ (\ mathbf = m \ mathbf = m \ stânga (\ dreapta). \) Atunci lucrarea pentru mișcarea corpului este egal \ [>> + Q \ frac> >> \ dreapta) dt >> = \ păcat \ alpha >> \ normalsize >>> - g \ cdot \ frac >>> \ dreapta) dt = >> <- g\int\limits_0^\sin\alpha>> \ Normalsize >>>> \ dreapta) dt = >> <- g\int\limits_0^\sin\alpha>> \ Normalsize >> = <- g\left[ \right|_^\sin\alpha>> \ Normalsize >> \ dreapta]> = <- g\left[ \sin \alpha \cdot t - \frac>>> \ dreapta)> \ dreapta | _ ^ \ păcatul \ alfa >> \ normalsize >> \ dreapta]> = <- g\left( ^2>\ Alpha >> - \ frac ^ 2> \ alfa >>>>> \ dreapta) = 0.> \] Acest rezultat se explică prin faptul că câmpul gravitațional al Pământului este potențialul, ca egalitatea \ [\ frac >> = \ frac >> = 0. \] Constatăm potențialul acestui domeniu. In termeni generali, este înregistrată ca \ [\ dreapta) = \ int + \ stânga (y \ dreapta)> = + \ stânga (y \ dreapta)> = + \ stânga (y \ dreapta).> \] Presupunând \ (\ mare \ frac >> \ normalsize = Q \ stânga (\ dreapta) = - g \) găsi \ [\ frac> \ stânga (y \ dreapta) = - g \; \; \ Rightarrow \ left (y \ dreapta) = - gy + \] Astfel, potențialul câmpului gravitațional este egal \ [u \ stânga (\ dreapta) = -. Gy + = C -. Gy \] unde \ (C \) - constantă care poate fi setat egal \ (0. \) rezultatul este un potențial \ [u \ stânga (\ dreapta) = -. gy \] Acest lucru arată că, atunci când corpul este mutat din punctul \ inițial (o \ left (\ dreapta) \) la punctul final \ (a \ stânga (\ dreapta) \) muncă este egal \ [W = u \ din stânga (a \ dreapta) - u \ stânga (O \ dreapta) = 0. \]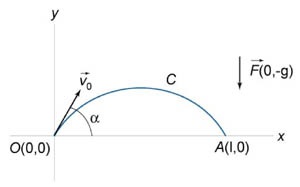
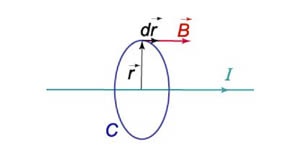
Se calculează inducția magnetică în vid, la o distanță \ (r \) de la axa unui infinit lung curent conductor \ (I. \)
Pentru a găsi câmpul magnetic la rasstonii \ (r \) de conductor, ia în considerare circulară raza de contur \ (r \) dispuse perpendicular pe conductorul de curent (figura \ (7 \)). Deoarece câmpul \ (\ mathbf \) este direcționat la o tangentă la conturul circular, în orice moment, produsul scalar al vectorilor \ (\ mathbf \) și \ (d \ mathbf \) este pur și simplu \ (Bdr. \) Atunci putem scrie \ [ \ oint \ limits_C \ cdot d \ mathbf> = \ oint \ limits_C = B \ oint \ limits_C = 2 \ pi rB \] rezultatul este o \ [2 \ pi rB = I \ ;. \; \ textul \; \; B = \ fracI >>>. \]
Valoarea Estimarea forței \ electromotoare (\ varepsilon \) și câmpul \ electric (E, \) care apar în raza inelului \ (1 \, \ textul \) la avioane de pasageri, în cazul în care zborul aeronavei într-un câmp magnetic cu o viteză a Pământului \ (900 \, \ text. \)
Conform legii lui Faraday \ [\ varepsilon = \ oint \ limits_C = -. \ Frac >> \] Deoarece conductive inel se mută la câmpul magnetic al Pământului, produce o modificare a fluxului magnetic \ (\ psi, \), care trece prin inelul.
Să presupunem că câmpul magnetic \ (\ mathbf \) perpendicular pe planul inelului. Apoi, în timpul \ (\ Delta t \) variația debitului este egal cu \ [\ Delta \ psi = 2rBx = 2rBv \ Delta t \] unde \ (x = v \ Delta t \) \ (v \) - viteza aeronavei, \ (B \) - câmpul magnetic al Pământului. Din ultima expresie obținem \ [\ varepsilon = - \ frac >> = 2rBv \.] Substituind valorile date \ [v = 900 \, \ text = 250 \, \ text, \; \ r = 1 \, \ text = 0,01 \, \ text \; \; B = 5 \ ori> \, \ text, \] găsi valoarea de emf \ [\ Varepsilon = 2rBv = 2 \ cdot 0,01 \ cdot 5 \ ori> \ cdot 250 = 0,00025 \, \ text. \] După cum se poate observa, este destul de sigur pentru pasageri.
Tension apare câmp electric este determinată de formula \ (\ varepsilon = \ int \ limits_C \ cdot d \ mathbf>. \) Prin simetrie, câmpul electric indus va avea o amplitudine constantă în orice punct în inel. Acesta este direcționat la o tangentă la inelul în orice punct. Acest lucru îl face ușor pentru a calcula linia integrală. \ [\ Varepsilon = \ oint \ limits_C \ cdot d \ mathbf> = \ oint \ limits_C = E \ oint \ limits_C = 2 \ rE pi. \] Prin urmare, intensitatea câmpului electric este egal cu \ [E = \ frac> = \ frac >> = 0,004 \, \ text. \]