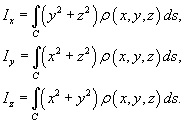2. Aplicații fizice ale integralelor
Integrale duble aplicații 2.1Fizicheskie
Masa și momentele de plăci statice
Să presupunem că placa plană este realizată dintr-un material neomogen, și ocupă regiunea R în planul Oxy. Lăsați densitatea plăcii la un punct (x, y) în R este egal. Apoi masa plăcii este exprimată printr-o integrală dublă în formă
Placă de cuplu static axa Ox relativă se determină prin formula
La fel este momentul static al plăcii în raport cu axa Oy.
Coordonatele centrului de masă al plăcii. ocupă regiunea R în planul Oxy la o densitate distribuită conform legii descrise de formulele

Pentru o placă omogenă cu densitate pentru toate (x, y) în centrul R masei este determinată doar de forma, iar zona este numită centroidului.
Momentele de inerție ale plăcii
Momentul de inerție al plăcii în raport cu axa Ox exprimată prin formula
In mod similar calculat moment de inerție plăcii în raport cu axa Oy.
Polar momentul de inerție al plăcii este
Să presupunem că sarcina electrică este distribuită pe regiunea R în planul Oxy și este dată funcția de densitate de distribuție. Apoi, taxa totală este dată de plastinyQ
Valoarea medie a funcției
Aici, de asemenea, formula Dyal calcularea unei valori medii a valorilor distribuite. Fie f (x, y) este o funcție continuă în regiunea R închis în planul Oxy. valoarea funcției μ f (x, y) înseamnă în zona definită de formula R
în cazul în care - zona R. regiunii de integrare
Se calculează momentele de inerție ale triunghiului delimitat de liniile drepte (figura 2) și care are o densitate.
Găsim momentul de inerție al plăcii în raport cu axa Ox.

În mod similar, vom calcula momentul de inerție în jurul axei Oy.
2.2 aplicatii fizice ale integralelor triple
Masa și momentele statice ale corpului
Lăsați corpul ocupă un volum de U și densitatea în vrac la punctul M (x, y, z) este dată funcția care p (x, y, z). Apoi masa telam se calculează cu ajutorul triplu integralei:
Momentele statice ale corpului în raport cu planul de coordonate Oxy, Oxz, Oyz exprimată prin formulele
Coordonatele centrului de greutate este dată de:
În cazul în care organismul este uniform, cu o densitate ρ (x, y, z) = 1 pentru punctul M (x, y, z) în centrul de greutate U. depinde de geometria corpului și se numește centroidului.
Momentele de inerție
Momentele de inerție la planul de coordonate Oxy, Oxz, Oyz sunt date de
și inerția momentelor despre axele Ox, Oy, Oz sunt calculate prin formulele
După cum se poate observa, relațiile
Momentul de inerție al corpului în raport cu originea este integrala
Momentul de inerție în raport cu originea poate fi exprimată în termeni de momente de inerție în raport cu coordonate planurile:
Acest tensor este simetrică și, prin urmare, poate fi redus la forma diagonală cu o anumită alegere a axelor Ox ", Oy, Oz. Valorile elementelor diagonale (după reducerea formei diagonală a tensorului) se numesc momentele principale de inerție. și a spus direcție - sau vectori proprii axe principale de inerție.
În cazul în care un organism se rotește în jurul unei axe care nu sovpadayushey cu axa principală de inerție, ea va experimenta vibrații la viteze de rotație mari. Prin urmare, atunci când proiectarea unor astfel de dispozitive este necesar ca axa de rotație coincide cu una dintre axele principale de inerție. De exemplu, atunci când se efectuează o anvelopă de vehicul de echilibrare înlocuirea lor: greutăți mici adăugate la roata pentru a oferi un meci cu axa de rotație a axei principale de inerție și pentru eliminarea vibrațiilor.
Potențialul gravitațional și forța gravitațională
potențial corp Newtonian la punctul P (x, y, z) este integrala
unde ρ (ξ, η, ζ) - densitatea corpului și.
Integrarea se realizează asupra volumului corpului. Cunoașterea potențialului poate fi calculată gravitațional punct material de masă m a corpului și a distribuit cu ρ densitate predeterminată (ξ, η, ζ) prin formula
unde G - constanta gravitațională.
Găsiți raza R. γ Densitatea masei sferei este proporțională cu pătratul distanței de la centru.
Prin ipoteză, y raportul densitate setat = y AR 2. în cazul în care o - este o constantă, r - distanța de la centru. Masa mingea este convenabil pentru a calcula coordonatele sferice:

2.3 aplicatii fizice ale Integrale curbilinii
Cu Integrale curbilinii calculate
Centrul de masă și momentele de inerție ale curbei;
Lucrul prin mutarea corpului într-un câmp de forță;
Câmpul magnetic în jurul unui conductor cu un curent (Legea lui Ampere);
inducție electromagnetică într-o buclă închisă cu fluxul magnetic (Legea lui Faraday).
Considerăm că acestea mai detaliat cu exemple de aplicații.
Să presupunem că o bucată de sârmă descrie o curbă spațială C. Să presupunem că masa este distribuită de-a lungul curbei cu o densitate care p (x, y, z). Apoi, masa totală a curbei este exprimată printr-o linie integrală de primul tip
Dacă curba C este dat în formă parametric utilizând o funcție vector, masa sa este descrisă prin formula
În cazul unei curbe plan definit în planul Oxy. Acesta este definit ca greutatea
sau în formă parametrică
Centrul de masă și momentele de inerție ale curbei
Din nou, lasa o bucată de sârmă este descrisă de o curbă C. și distribuția masei de-a lungul unei curbe continue densitate definită funcție ρ (x, y, z). Apoi coordonatele centrului de masă al curbei definite prin formulele
- așa-numitele momente de prim ordin.
Momentele de inerție în jurul axelor Ox, Oy și Oz sunt definite de