3.1. Ortogonale (dreptunghiular) punctul de proiecție. Proiectarea unui punct de pe cele trei planuri ale proiecțiilor
Să considerăm un sistem de trei planuri reciproc perpendiculare ale proeminențelor (Figura 5.): P1 plane de proiecție orizontală, un plan P2 frontal și proiecție P3 proiecții profile plane.
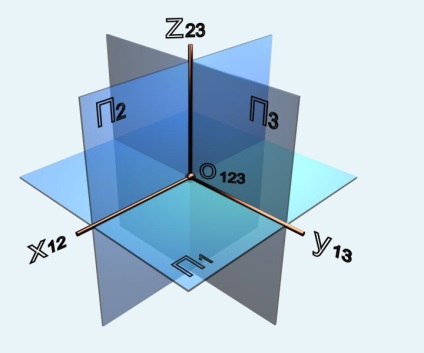
Fig. 5. Planul de proiecție:
Punctul de intersecție a trei avioane O123 - origine. Linia de intersecție planuri orizontale și frontale numite x12 = axe de coordonate A1 ∩ A2. intersecția liniei orizontale și profilul se numește axa planelor de proiecție Y13 = P1 ∩ P3. intersecția frontală și avioane de profil se numește axa de Proiectări Z23 = A2 ∩ A3.
Având în vedere că planul de proiecție sunt infinite, trei avioane împart întregul spațiu în opt părți - octante. Ordinea octante de referință (a se vedea figura 5 ..) la stânga P3 plane (în sens antiorar) de la primul la al patrulea, spre dreapta - a cincea a opta.
Direcția axelor x, y, z în primul Octant este considerat pozitiv. Semne axe, a continuat Pentru origine, este considerat negativ.
Pentru a obține puncte de proiecție A pe cele trei planuri (fig. 6) A1. P2 și P3 sunt efectuate prin punctul A raze proeminente [AA1) - până la intersecția cu planul P1. [AA2) - până la intersecția cu P2 și planul [AA3) - până la intersecția cu P3 avionul. Punctul A1 - proiecție orizontală a punctului. A2 - punctul de vedere din față. A3 - profil punctul de proiecție. Puncte A12 A13 A23 - auxiliar, respectiv, situată pe axele x, y, z.
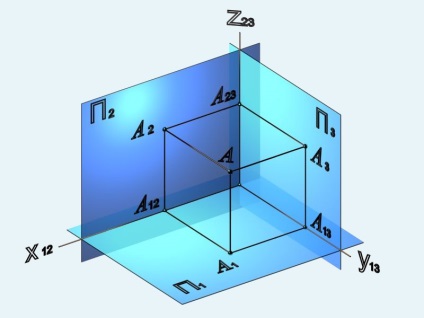
Fig. 6. Proiectarea trei puncte pe planul de proiecție
Pentru plat punct desenul A pentru a roti planul P1 jurul axei X în sensul acelor de ceasornic, iar planul P3 - în jurul axei z pentru a se alinia cu P2. P2 plan. A2 și A12 rămân punctul (Fig. 7), A1 și A13 punct axa y1 și sunt rotite împreună cu A1 fix. După rândul său, punctul A1. A2 și A12 formează o legătură verticală. Punctele A3 și A23. împreună cu axa de cotitură P3 și Y3. formă, după rotire, orizontală legătură A2 A3. Punctele A1 și A3 sunt conectate printr-o linie întreruptă conexiunea A0 A1 A3. Partea de sus a unui link rupt sau punctul de refracție A0 se află pe bisectoarea unghiului O123 Y3 y1. Setul de noduri de conexiune polilinii specifică o linie condiționată, numită constantă directă complex desen k123.
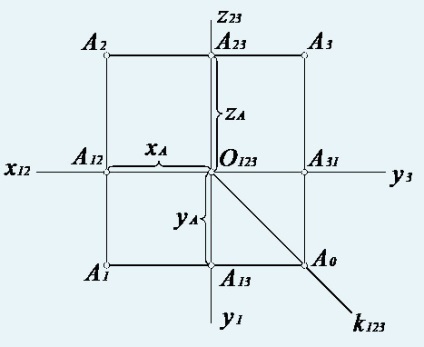
Fig. 7. Trehkartinny integrat punct de desen:
Desen de trei planuri suprapuse proiecții numite trehkartinnym desen complex. complexă metodă de formare desen se numește Monge, după savantul francez Gaspard Monge, care a trăit în secolul al XIX-lea, în primul rând a sugerat utilizând combinații de desene.
Pentru a rezolva problemele din desenele geometriei descriptive sunt adesea folosite pe două planuri suprapuse ale proeminențelor, care sunt numite desene complexe dvuhkartinnymi (Fig. 8).
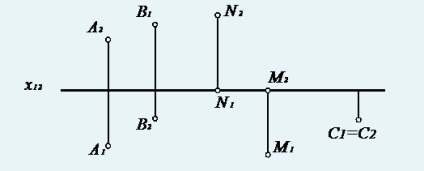
Fig. 8. Dvuhkartinny punct de desen integrat care ocupă o poziție diferită în raport cu planurile de proiecție