Cifrele de construcții de proiecție plane (t. E. Cifrele, toate punctele din care se află într-un plan, de exemplu, un pătrat, cerc, elipsa și altele. D.) este redus la construcția proeminențelor o serie de puncte, segmente de linie dreapta si linii curbe care formează contururile figurilor proiecțiilor. Cunoscând coordonatele nodurilor, de exemplu, un triunghi, se poate construi proiecțiile acestor puncte, atunci laturile proeminenței și astfel se obține forme de proiecție.
Desenele conțin proiecția triunghiului au cunoscut (de exemplu, Fig. 110, 112 și colab.). Dacă vom compara cifra. 110 și 112, se poate observa că în Fig. 110 una dintre proeminențele, un set de față, prezintă partea „față“ a triunghiului și orizontală - „înapoi“ A din Fig. Fiecare dintre proeminențele 112 prezintă un triunghi cu aceeași parte a acesteia. Semn poate fi înfășurării ordinea nodurilor: Fig. 110 pentru proiecția frontală în sensul acelor de ceasornic (numărând de la A „la C“) și pentru orizontală - în sens antiorar; Fig. 112 ocolind atât proiecțiile în doar o singură direcție - în acest caz sensul acelor de ceasornic.
În general, în π1 sistem. π2. π3 proiecția unui poligon sunt, de asemenea, poligoane cu același număr de părți; în care planul poligonului este o poziție comună plan. Dar dacă sistemul π1. π2 ambele proiecții, de exemplu, triunghiul este un triunghi, planul său poate fi un plan sau profilat generic proeminente: Fig. 112 - plan poziția generală, și Fig. 127 - se proiectează în profil. Determinant este, așa cum sa menționat la p. 52 în explicarea Fig. 127, orizontală (sau frontal) în cazul în care proiecția pe π1 și π2 sunt reciproc paralele, planul-proiecție profil (Figura 127.); dacă nu paralel, planul generic (de exemplu, Fig. 112, 115, stânga).
Dacă proiecția poligonului pe π1 sau π2 este un segment de linie, planul care este perpendicular pe poligon, respectiv π1 sau n2. De exemplu, în Fig. 123 plan al triunghiului proetsiruyu- orizontal schaya, în Fig. 125 --față proeminentă.
Figura dispuse paralel cu planul de proiecție este proiectat să-l fără distorsiuni. De exemplu, toate elementele triunghiului CDE, prezentat în Fig. 133, proiectat pe piață. π2 fără distorsiune; cercul prezentat în Fig. 140 este proiectat pe pătrat. π1 fără distorsiuni. -
Dacă planul figurii nu este paralelă cu planul de proiecție pentru a determina forma naturala (m. E. Fără distorsiuni) a figurii metodele specificate în continuare se aplică, capitolul V. Desigur, s-ar putea acum, fără să știe aceste metode de a construi, de exemplu, aspectul natural al triunghiului prezentat în Fig. 112, care definește lungimea fiecăreia dintre laturile sale ca lungimea segmentului (cm. § 13) și apoi construirea unui triunghi pe segmentele găsite. În același timp, a fost determinată și unghiurile triunghiului. Cosi, de exemplu, în construcția de scanare
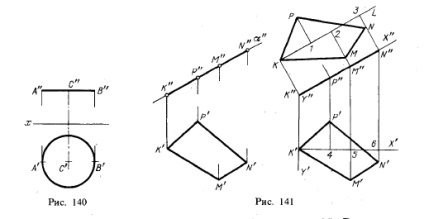
suprafața laterală a unei piramide, prisme și colab. (cm. Mai departe § 44). Dacă poligonul este situat în proiectarea planului, putem construi aspectul său natural așa cum este prezentat în Fig. 141.
Să presupunem că doriți să definiți aspectul natural al KPNM patrulater, situată în piața din față-proeminentă. α. Apoi, așa cum se arată în Fig. 141 spre dreapta, puteți lua în planul figurii două axe de coordonate rectangulare cu începutul, cel puțin la punctul K; 2. Axa abscisei ordonata perpendicular pe π2 (proiecția acestei axe K „Y“, K'Y „), trage o linie dreaptă KL (acest lucru se poate face, de exemplu, paralel cu«X») și puneți-l pe K1 = K„R "K2 = K" M "SC = K" N. " Apoi, pe perpendicularele la linia KL la punctele 1,2 și 3 amâna segmentele P1 = R'4, M'5 și M2 = N3 = N'6. Construit KMNP astfel, patrulater reprezintă un aspect natural predeterminat.
În rezolvarea multor probleme pe care problema ce poziție o figură plan în ceea ce privește planurile de proiecție, devine esențială. Ca un exemplu, ia în considerare problema de a construi patru Triangle Center.
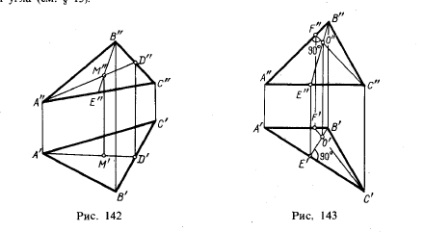
Deoarece segmentul de linie diviziune în spațiu corespunde jumătății aceeași divizie a porțiunii de proiecție (vezi. § 12), construcția punctului de intersecție al medianele triunghiului 1) poate fi produs în figură, în toate cazurile în mod direct. Destul (Fig. 142), mediana cheltui pe fiecare dintre proiecțiile triunghiului și punctul de intersecție al medianele sale vor fi determinate. Astfel, este posibil să se limiteze construcția ambelor proeminențelor numai o mediană (de exemplu, A'D „și A«D») și o a doua proeminență mediană (de exemplu, V«E»); în intersecția A „E„D“și B«obținem punctul M», și de la ea pentru a găsi A'D«punctul M».
Ar putea fi, de asemenea, construind doar unul dintre medianele triunghiului, bazat pe acesta găsi punctul M asupra proprietăților cunoscute ale geometriei punctului (care împarte fiecare mediană față de 2 1).
Construcția punctului de intersecție al celor trei altitudini ale unui triunghi 2) și punctul perpendicular pe laturile triunghiului trasate prin mijlocul 3) legate de liniile perpendiculare reciproc.
1) Punctul de intersecție al medianele triunghiului este centrul de greutate.
2) orthocenter triunghi.
3) Centrul cercului circumscris.
În § 15 au fost specificate condițiile în care segmentele de linie perpendiculare în spațiu sunt proiecțiile sale sunt de asemenea perpendiculare pe segmentele, dacă planul triunghi paralel cu planul de proiecție (de exemplu, CDE triunghi în Fig. 133), apoi, scăzând perpendicularele din punctele C „D“ și E „pe partea opusă a acestuia, vom obține înălțimea de proiecție a triunghiului, ci într-un triunghi generic astfel încât să nu poți să faci,
În cazul particular în care o latură a triunghiului este paralelă cu pătrat. π1; iar celălalt PIBpp paralel, π2 (fig, 143), având C "F" perpendicular "B" A și V'E 'perpendiculară pe A'C' ajunge în spațiul și CF⊥AV BE⊥AS; înălțimi punct de intersecție a fost construit fără tehnici speciale.
În același caz general pentru desfășurarea în proiecția desenarea liniilor perpendiculare pe care trebuie să recurgă la tehnici speciale, care vor fi descrise în continuare.
Construirea punctul de intersecție al Bisectoarele triunghiului 1) poate fi produs direct numai în cazuri speciale, poziția triunghi în raport cu planurile de proiecție. Acest lucru se datorează faptului că un unghi de împărțire în două proiecție de împărțire în două răspunde în spațiul numai în cazul în care unghiul dintre laturile sunt la fel de înclinate în raport cu planul de proiecție pe care proiecții produse unghi de împărțire în două (a se vedea. § 15).
În construirea proiecțiile unui poligon trebuie să acorde o atenție să nu încalce o condiție de a găsi toate punctele de figura în același plan
Fig. 144 sunt complet proiecția orizontală a unui pentagon ABCDE și proiecție frontală a doar trei dintre nodurile sale: A „B“ și E“, pe dreapta
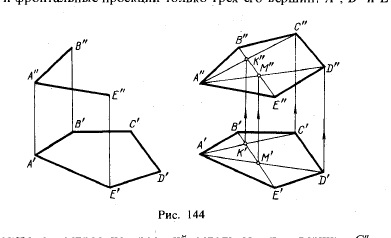
Figura 144 ilustrează structura proeminențelor celorlalte două vârfuri, C „și D“, un pentagon, la punctele C și D se află în planul definit de trei puncte A.
1) Centrul cercului inscris.
B și E, este necesar ca acestea au fost pe liniile situate în planul acestor linii sunt diagonala AC, AD și BE, proiecția orizontală pe care putem construi. Pe proiecția frontală a pentagonului putem trage doar în „E“, dar în planul pentagonului sunt punctele de intersecție a diagonalelor K și M, proeminențele orizontale (K „și M“) sunt disponibile, iar proiecția din față, obținem o dată, deoarece acestea trebuie să se bazeze pe B "E". Două puncte sunt construite proiecție frontală, iar celelalte două diagonale A „R“ și A „M“, ei trebuie să se afle punctele C „și D“, care sunt definite de proiecțiile lor orizontale.
Cerc al cărui plan este paralel cu un plan de proiecție este proiectat pe acest plan, fără distorsiuni (a se vedea, fig, 140, în care cercul este luat într-un plan orizontal). Dacă planul cercului perpendicular pe planul de proiecție, atunci acest plan este proiectat ca un segment de linie cerc egal cu diametrul cercului,
Dar dacă cercul este situat în planul care constituie planul de proiecție a unui unghi ascuțit φ, intervalul de proiecție este o figură numită elipsă.
Elipsa este numită și curba de separare elipsă formă, dacă cifra este o proiecție gama elipsa, Ellipse-line este o proiecție a unui cerc. În cele ce urmează, atunci când se vorbește de elipsei, ne referim la proiecția unui cerc.
Elipsa se referă la numărul de curbe este o curbă de ordinul doi. Ecuațiile curbelor în coordonate carteziene reprezintă oa doua ecuație ordine. Curba a doua ordine se intersectează cu linia dreaptă, la două puncte. În continuare, ne vom întâlni din nou cu parabolei și hiperbola, prea, curbele de ordinul al doilea.
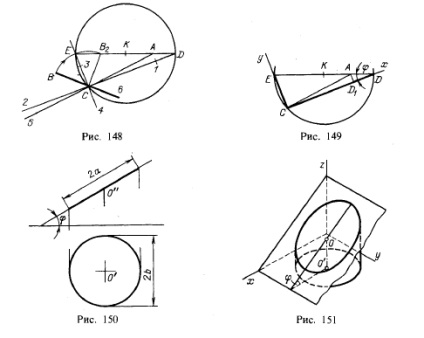
Elipsă poate fi considerat ca fiind „compresie“ cerc. Acest lucru este prezentat în Figura 145, spre stânga, pus pe o rază OB OB1 întârziată segment de lungime b, în care b 1) la elipsa în punctul K.
1) De la normalis (lat.) - o linie dreaptă.
Cum de a construi axa elipsei, dacă știți că diametrele sale conjugate?
Fie C obținută conjugat semi-axe A și CB (Fig. 148). Pentru a construi axele elipsei:
- una dintre semi-axele de conjugat, de exemplu, NE, pivotat printr-un unghi de 90 ° față de celălalt (în poziția CB2);
- AB2 segmentul de cheltuieli și împărțiți-l în jumătate;
- din punctul de la COP sârmă raza cercului;
- definite direct AB2 segment. continuă până la intersecția cu acest cerc în punctele D și E;
- efectua DC directă, pentru a primi direcția axei majore;
- Modul de desfășurare a UE - direcția axei mici a elipsei;
- Noi amâne C1 = AE - axa semimajore;
- Noi amâne SOC = AD - axa minoră;
- Noi amânăm C2 = C1 și C4 = NW, C5 = CA, CB = Sa.
Elipsa poate fi realizată prin opt puncte 1, A 3, B, 2, 5, 6 sau 4 și este construit pe axele majore și minore așa cum se arată în Fig. 147.
Deci, petrece un CD direct și CE, avem direcția axelor majore și minore ale elipsei; punctul A diametru elipsă aparținând ED împarte în două segmente, dintre care unul (AE) este axa semimajore a elipsei și celălalt (AD) - axa mică. Dacă (Fig. 149)
ia axele de coordonate x și y, respectiv pentru CD direct și CE și de la punctul A pentru a efectua AD perpendicular pe linia CD, coordonatele punctului A poate fi exprimată după cum urmează:
Această ecuație este o elipsă a cărei AE - axa semimajore, un AD - axa minoră.
Fig. 146 ilustrează structura a fost proiecția orizontală amplasată circumferențial în proiecție frontală-planul înclinat spre pl. π1. Să presupunem acum că într-un astfel de plan este o elipsă cu semi-axe a și b. proiecția sa poate fi, uneori, un cerc cu un diametru egal cu axa mică a elipsei: Aceasta se va întâmpla atunci când pentru unghiul dintre planul în care se află elipsei și pătrat. π1 cos de relații? = B / a (Fig. 150).
Circumferința rezultată a proiecției va servi un număr de elipse, dacă unghiul cp pentru a schimba dimensiunea și a, b lăsând neschimbat. Imaginati-va un cilindru circular drept cu o axă verticală (Figura 151.); secțiunea înclinată a cilindrului sunt elipse, axa secundară este egală cu diametrul cilindrului.
Întrebări pentru §§20-21
- Așa cum este ilustrat în desen-frongalno proiectând plan tras prin poziția generală directă?
- Cum de a construi o proiecție a centrului de greutate într-un anumit desen triunghi?
- Ceea ce poate fi un interval de proiecție, în funcție de poziția de planul său în raport cu planul de proiecție?
- Putem considera elipsei ca o „comprimare“ cerc?
- Care este raportul de aspect al elipsei?
- dacă elipsa are: a) axa de simetrie, b) un centru de simetrie?
- Care sunt diametrele unei elipse se numesc: a) axe, b) diametre de conjugat?
- Așa cum se specifică prin diametrele conjugate ale elipsei pentru a construi axei sale?