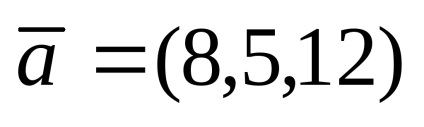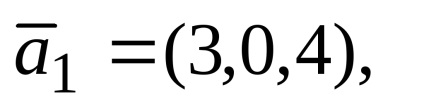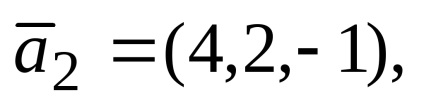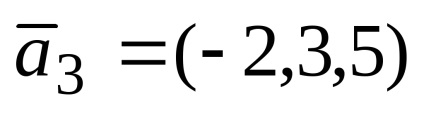aritmetică vector n-dimensional
aritmetica n-dimensional vector este un set ordonat de numere reale n, iar numerele incluse în acest set sunt numite coordonate vectoriale.
Numărul de componente ale vectorului se numește dimensiunea sa.
Dacă toate coordonatele vectorului sunt zero, numit vectorul zero și este notat cu 0 sau

Dacă coordonatele corespunzătoare iravny vectori, vectorii nazyvayutsyaravnymi:
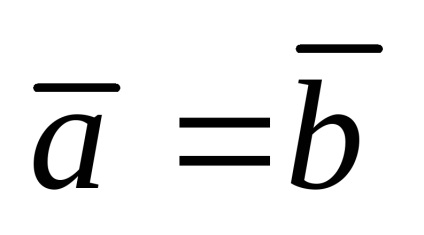

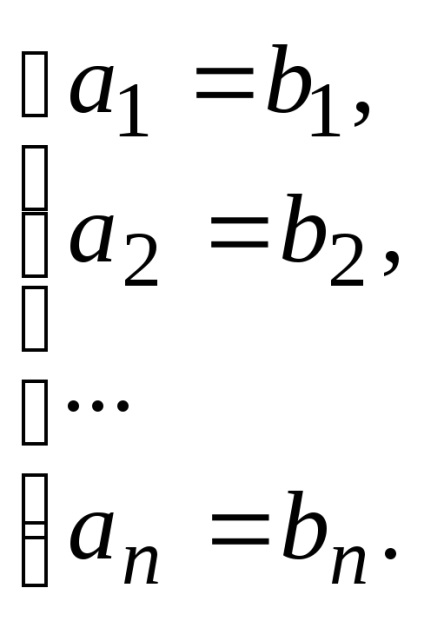
Cele mai simple de operații cu vectori n-dimensionale sunt vector adunare, scădere și multiplicarea vectorilor vectorului de un număr. Astfel de operații sunt numite liniare. Adăugați și vectori scădeți pot fi doar aceeași dimensiune.
Suma (diferența) a doi vectori n-dimensionali inazyvaetsyan vector dimensional
vector dimensional Proizvedeniemn printr-un număr

.
Astfel, prin adunarea sau scăderea vectorilor sunt adăugate sau scăzute aceleași coordonate. Când înmulțirea fiecărui vector cu un număr de coordonate al vectorului este înmulțită cu acest număr.
Setul de vectori n-dimensionale cu ea înscrise operațiile de adunare, scădere și vectorul de înmulțire cu un număr numit spațiul vectorial n-dimensional și aritmetică notată
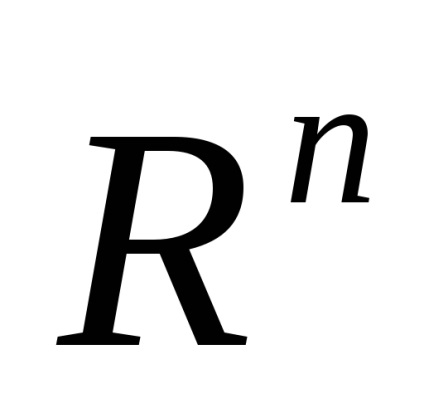
Dependența liniară a vectorilor
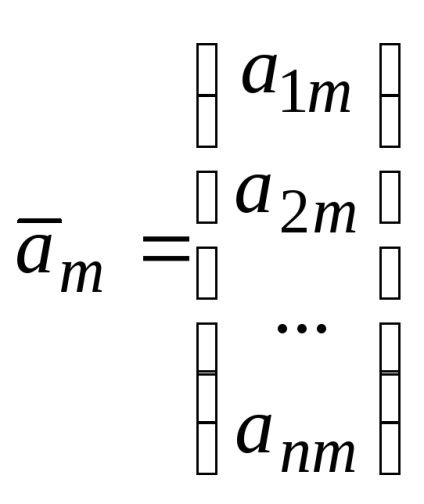
Să fie o mn-dimensională de vectori
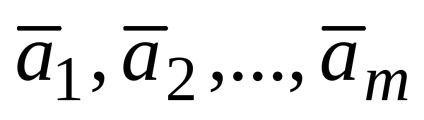
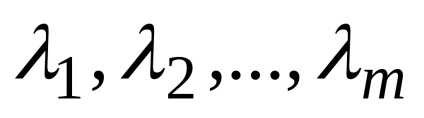
Se numește o combinație liniară a vectorilor
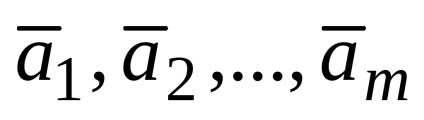
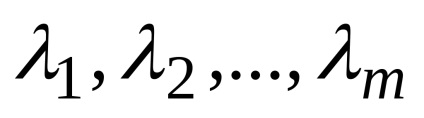
O combinație liniară de vectori n-dimensionale este, de asemenea, un vector n-dimensional.
vectori
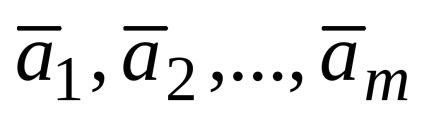
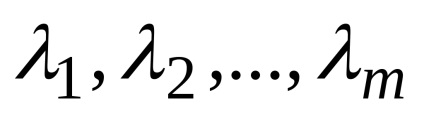
.
În cazul în care această egalitate este posibilă numai atunci când toate numerele
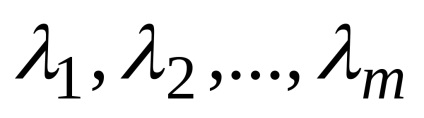
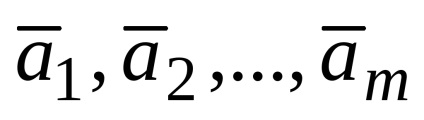
vectorii luata in considerare
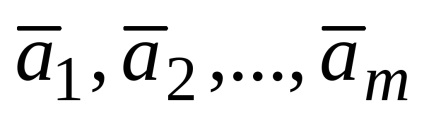
Dacă un vector

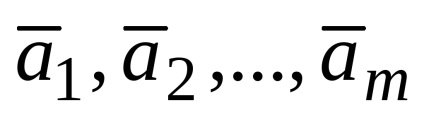
,
a extins sistemul de vectori este liniar dependent. Pe de altă parte, în cazul în care sistemul de vectori
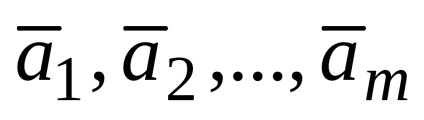
Astfel, starea de dependență liniară a vectorilor pot fi formulate după cum urmează: sistemul de vectori este liniar dependent dacă și numai dacă cel puțin unul dintre un sistem de vectori este o combinație liniară de alți vectori.
Vectorii de bază și sistemul de rang
Având în vedere un sistem de vectori
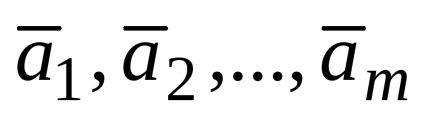
sistem de vector poate avea mai multe baze. În acest caz, toate conțin același număr de vectori.
Rangul unui sistem de vectori este numărul de vectori în orice bază a sistemului. Cu alte cuvinte, gradul de vectori egal cu numărul maxim de vectori de sistem liniar independent.
spațiu Bazisomn vector dimensional este un set de vectori liniar independenți n în acest spațiu.
Vector de descompunere a sistemului de vectori
Să fie un sistem de vectori
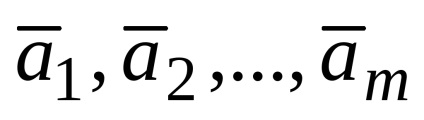
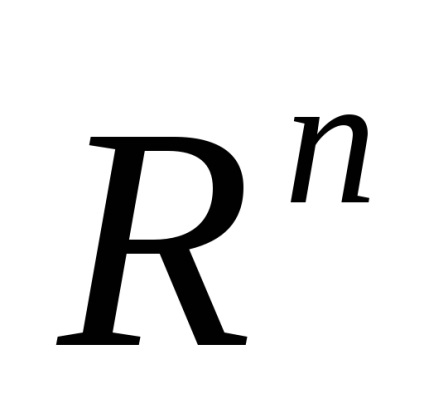
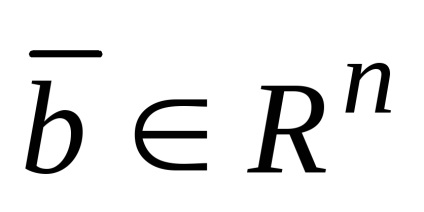
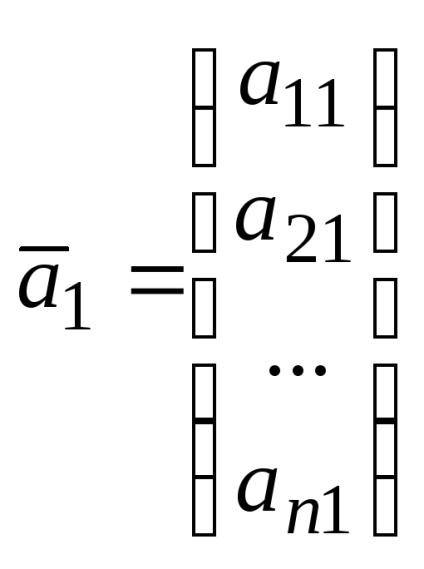
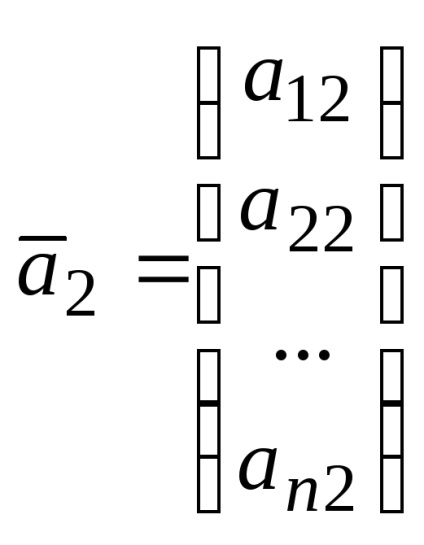
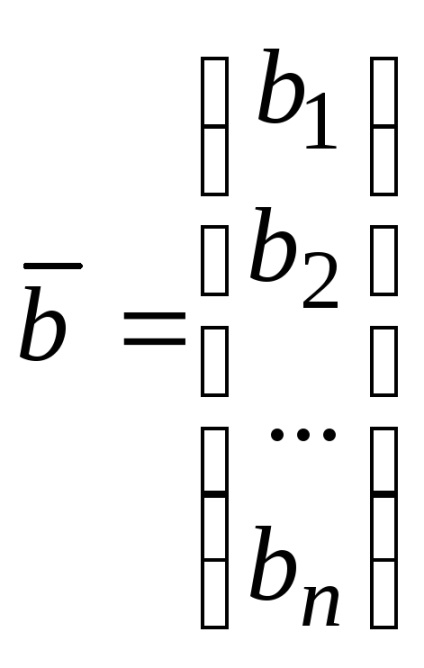
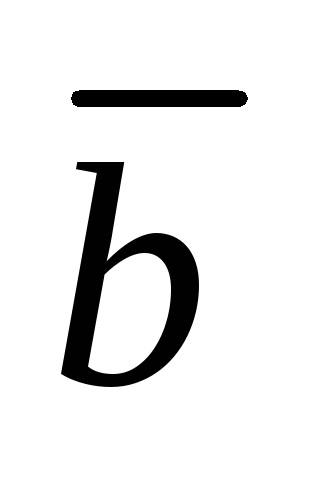
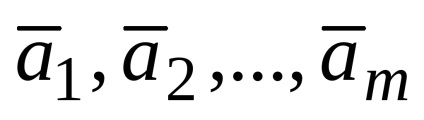
.
Această înregistrare se numește descompunere vector
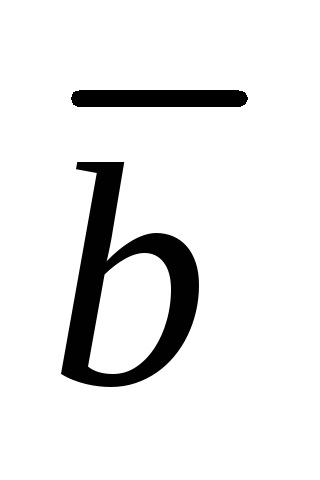
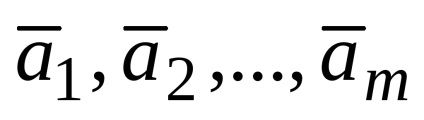
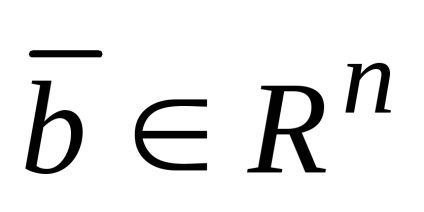
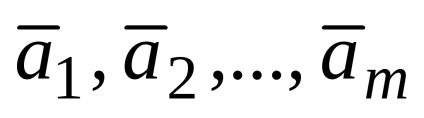
Scriem acest lucru sub formă de combinație liniară:
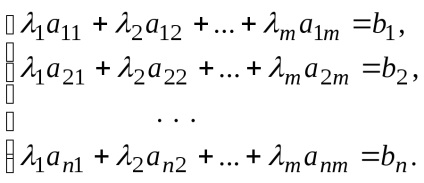
Un sistem de n ecuații cu m variabile
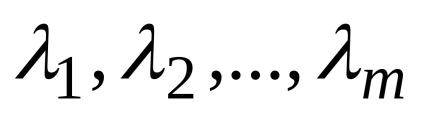
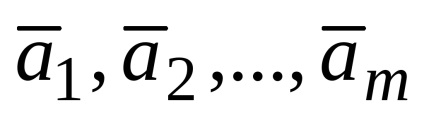
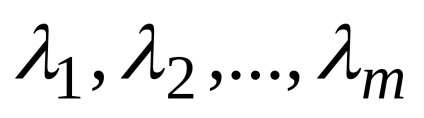
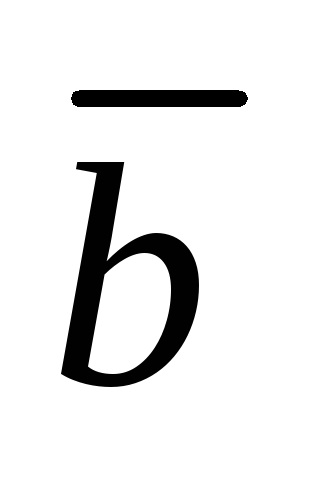
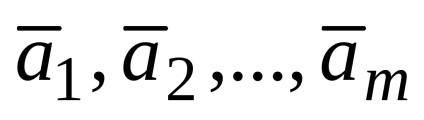
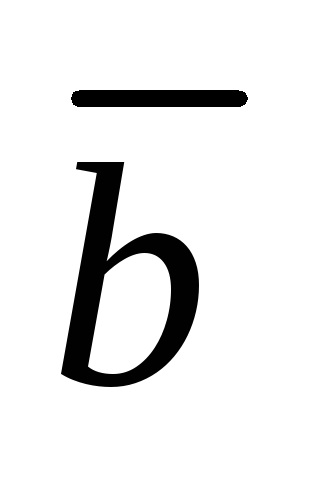
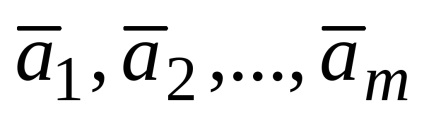
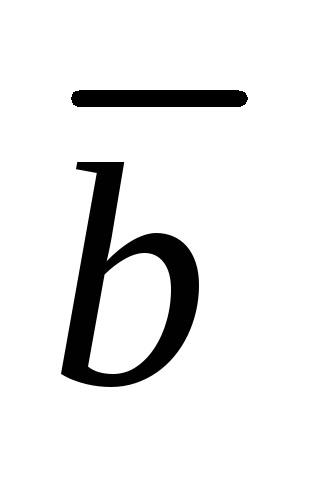
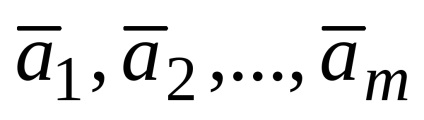
Astfel, reprezentarea vectorului ca o combinație liniară a vectorilor este echivalentă cu rezolvarea unui sistem de ecuații liniare.
Lăsați vectorii
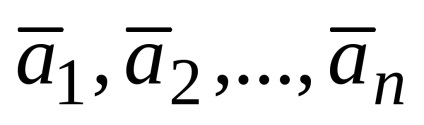

Exemplul 1. vectorii date
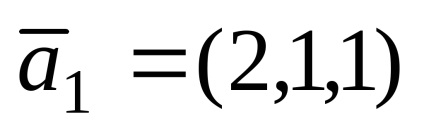
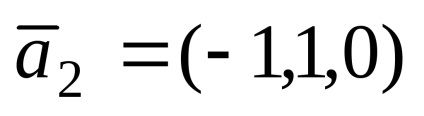
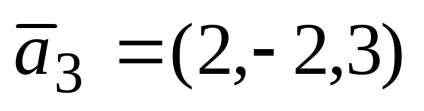
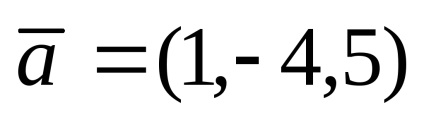
Decizie. Prin starea problemei vectorului

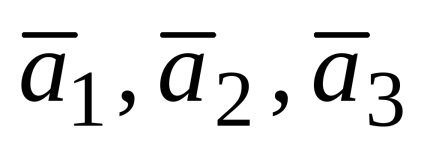
Un sistem de trei ecuații cu trei variabile
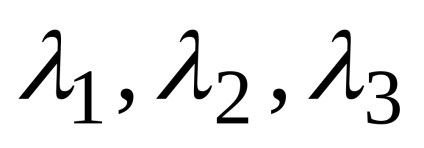
Întrebări pentru auto-cunoaștere
Ceea ce se numește un vector de aritmetica n-dimensional?
Determinate de suma diferenței dintre doi vectori n-dimensionale și produsul vectorului n-dimensional cu un scalar?
Ce este o combinație liniară a vectorilor m?
Care este sistemul de vectori se numește liniar dependentă și independentă liniar?
Ce se înțelege prin descompunerea vectorului de vectori ai sistemului?
Ceea ce se numește o bază a sistemului și vectorii de bază ale spațiului?
Sarcini de muncă independentă
Sunt vectori care formează o bază de spațiu bidimensional. vector descompus
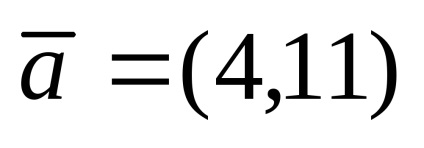
vector descompus