Un sistem de ecuații diferențiale ordinare pot fi reprezentate în următoarea formă generală:
Sau în formă vectorială:
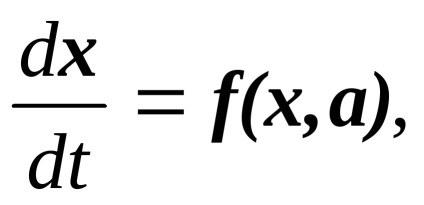
soluția de sistem este un set de funcții care satisfac ecuația inițială. Soluția poate fi scrisă în ecuațiile vectoriale formeSistema
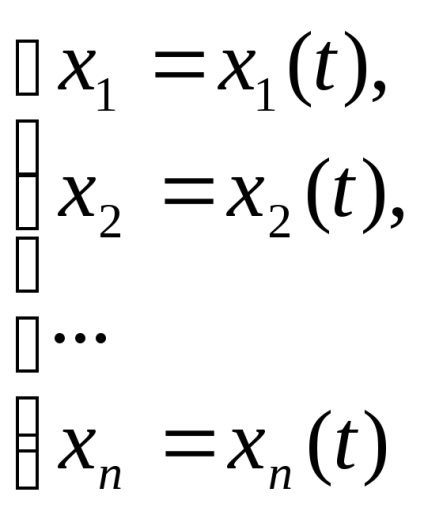
Este o ecuație curbă parametrică în spațiul n-dimensional al axelor reale. Această curbă nazyvayutfazovoy traiectorie a sistemului de ecuații diferențiale. În cazul i = 1,2,3 traiectorie oferă o reprezentare vizuală a comportamentului soluțiile corespunzătoare acesteia (fig. 3.2).
Ris.3.2.Resheniya și faza traiectorie a sistemului de ordinul doi
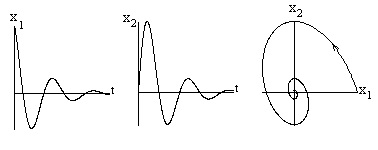
Setul de toate sistemele de traiectoriile de fază formează vfazovy portret al sistemului. Astfel, sistemele spațiale prostranstvonazyvayutfazovym. Astfel, spațiul de fază reprezintă setul de toate stările posibile ale sistemului dinamic. Fiecare nouă stare a sistemului corespund diferitelor puncte ale spațiului de fază.
Soluția sistemului de ecuații diferențiale determină evoluția studiului sistemului dinamic în timp. Această evoluție este reprezentată de mișcarea punctului de fază a traiectoriei corespunzătoare. Starea sistemului în momentt depinde nu numai de timp, dar, de asemenea, cu privire la starea inițială în care sistemul se află în momentul respectiv. Această din urmă condiție nazyvaetsyanachalnym relație pentru rezolvarea sistemului.
cale posibilă constând dintr-un singur punct: acesta este un punct de punct ilistatsionarnye de odihnă. puncte de odihnă sunt caracterizați prin aceea că derivații de timp ale variabilelor la aceste puncte sunt zero. Pentru a tochkabyla punctul de odihnă, este necesar și suficient pentru a se conforma cu termenii.
În cazul în care traiectoria trece de două ori prin același punct, această cale închisă, care se numește ciclu. și soluția corespunzătoare va fi periodic.
Astfel, există trei tipuri de trasee. neinchise, închise (cicluri) itochki odihnă. Fiecare punct al spațiului de fază este deținută de exact o singură cale. Prin urmare, în cazul în care două traiectorii de fază au un punct în comun. atunci ele coincid.
Rețineți de asemenea, că tipul de sistem
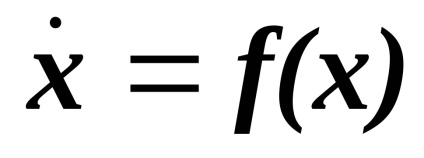
Construcția de portrete de fază
Să ne întoarcem la modelul sistemului mecanic așa cum este descris în Exemplul 3.1. Ecuația unui model neliniar este
.
Din ordinul doi ecuație poate merge la sistemul autonom al formei
,
Dacă acum în sistem pentru a elimina timpul t. Obținem sistemul de ecuații diferențiale în traiectoriile plane de fază
putem rescrie ultima ecuație după cum urmează:
Apoi, presupunând că în cazul în care, și după integrarea ecuației în cadrul egalității otdopoluchaem
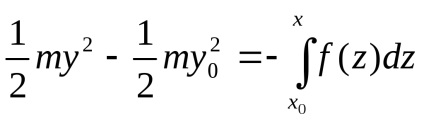
care poate fi rescrisă după cum urmează:
Rețineți că există o formulă pentru energia cinetică a unui sistem dinamic, și
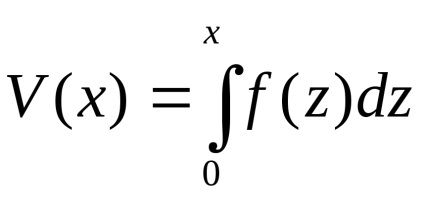
- Formula este energia sa potențială. Astfel, ecuația exprimă legea conservării energiei:
undeva energia totală a sistemului.
Este clar că această ecuație - ecuația traiectoriilor de fază ale sistemului conservator neliniar, deoarece se obține prin integrarea ecuației
Astfel, diferite valori ale fazei E plane corespund diferitelor curbe de energie constantă. Puncte staționare ale sistemului sunt punctele M * (x *, 0). gdex * - rădăcini. În acest caz, în cazul în care rescrierea legii de conservare a energiei sub formă de
,
puteți construi cu ușurință traiectorii de fază.
considerații generale Efectuat fac posibilă investigarea ecuația de mișcare a pendulului în mediu fără nici o rezistență, care are forma
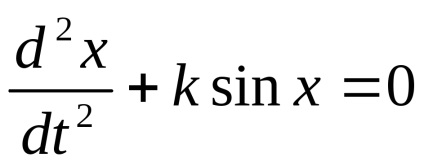
Deoarece ecuația este un caz special al ecuației, aceasta poate fi interpretată ca ecuația care descrie mișcarea liniară a masei corporale unitate fără frecare sub acțiunea arcurilor neliniare, în care forța de revenire este egal. În acest caz, sistemul de sine stătător, corespunzător ecuației, scrisă sub forma
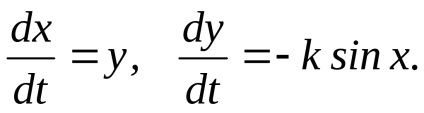
puncte singulari aici va fi un sistem de ecuații diferențiale de traiectorii de fază vor lua forma
Separând variabilele din ecuația finală și integrarea, obținem ecuația traiectoriilor de fază
Ultima ecuație este un caz special al legii de conservare a energiei, în cazul în care energia potențială este dată de
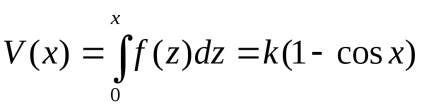
După determinarea valorii, putem schița o imagine schematică a comportamentului traiectoriilor în planul de fază, dacă vom folosi raportul.
Rezultante show fază portret (Fig. 3.3), în cazul în care otdo schimbări energetice, traiectoriile de fază corespunzătoare sunt închise, iar ecuația are soluții periodice. Pe de altă parte, în cazul în care, traiectoriile de fază corespunzătoare nu sunt închise, iar ecuația are soluții periodice. Valoare plan de fază soție corespunde traiectoriei de fază, care separă cele două tipuri diferite de mișcare, astfel de traiectorie nazyvayutseparatrisoy. traiectorii de fază de ondulare situată în afara separatrices corespund mișcării de rotație a unui pendul și trasee situate în zonele delimitate de separatrices închis - propunerea vibraționale.
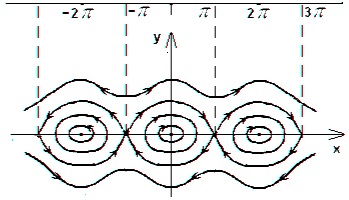
Fig. 3.3. Faza portret al sistemului conservator neliniar
In figura 3.3 se observă că în vecinătatea punctelor fixe traiectorii de fază gdepovedenie diferite de comportamentul de fază a traiectoriilor în vecinătatea punctelor fixe, unde
Să vedem acum ce influențează comportamentul traiectoriilor de fază ale sistemului conservativ de frecare liniară. În acest caz, ecuația devine
Fig. 3.4.Fazovye portrete sisteme conservative cu frecare
Ce sistem va avea un non-conservatoare. În cazul în care frecarea este suficient de mic, și anume posibile oscilații ale pendulului în raport cu poziția de echilibru, se poate demonstra că traiectoriile de fază sunt așa cum este prezentat schematic în figura 3.4, a. Dacă frecarea previne orice oscilație a pendulului în raport cu poziția de echilibru, modelul traiectoriilor de fază va avea forma prezentată în Fig. 3.4, b.
Dacă vom compara acum portretul de fază a unui sistem conservator cu ultimele două portrete de fază de sisteme non-conservatoare, se poate observa că traiectoriile de fază închise în frecare redusă, mutat într-o spirală, și cu o frecare puternică - în calea care fac parte din punctele singulare în anumite direcții.
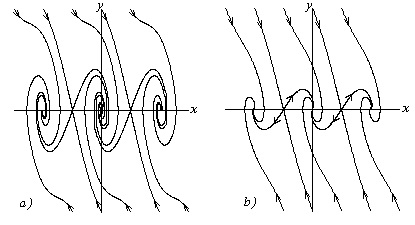
Fig. 3.4.Fazovye portrete ale sistemelor cu frecare:
frecare mică a-; b- frecare ridicată