Orice semnal poate fi descompus în componente. Acest semnal este numit descompunerea spectrală. Semnalul poate fi reprezentat ca un grafic al parametrilor semnalului de frecvență, o astfel de diagramă se numește semnalul spectrală sau spectru.
semnal Spectrum - un set de componente de semnal simple cu amplitudini precise, frecvențe și faze inițiale.
Aceasta semnale între spectrul și forma ei există o corelație puternică: schimbarea rezultatelor formei de undă într-o schimbare a spectrului său, și invers, orice schimbare în spectrul semnalului conduce la o schimbare în forma sa. Este important să ne amintim, ca transmiterea semnalelor într-un sistem de transport, acestea pot fi modificate, deoarece aceasta înseamnă că transformarea spectrele lor.
Există două tipuri de grafice spectrale:
- diagrama spectru amplitudine;
- diagrama de fază spectrală.
Amplitudinile diagrama spectrale - prezinta toate componentele cu amplitudini și frecvența acestora.
Diagrama de fază spectrală - prezintă toate componentele fazelor și frecvențele lor inițiale.
Orice semnal are o diagramă spectrală a amplitudinilor spectrale, și o diagramă de fază, în care structura poate conține o multitudine de componente.
Indiferent de spectrul (amplitudine sau fază), este reprezentat ca o pluralitate de linii - componente. În spectrul liniei spectrale amplitudinilor înălțime egală cu amplitudinea componentei semnalului și un spectru de fază - componenta de fază inițială. Mai mult decât atât, în spectrul amplitudinilor tuturor componentelor sunt pozitive, iar spectrul de fază, atât pozitive cât și negative. În cazul în care componenta spectrală de amplitudine este negativ, este luat spectru modulo amplitudinea și spectrul de fază a unei componente semn este inversată.
Semnale de spectru Clasificare.
1. Conform spectrele de tip sunt discrete (exclus) sau solid.
Un spectru discret, în care pot fi identificate componentele individuale.
spectru continuu este, care nu se pot separa componentele individuale, deoarece acestea sunt situate suficient de aproape pentru a fuziona unele cu altele.
2. distinge spectre de frecvență gama de mărginit și nemărginit.
Spectrum este limitat, la care întreaga energie a semnalului (toate componentele spectrale) sunt într-un interval de frecvență limitată (fmax.).
Gama este nelimitată, în care toată energia semnalului este gama de frecvență nelimitată (fmax.). În practică astfel de spectre limitate.
Reprezentarea spectrală a semnalelor periodice
1. Oscilația armonice.
Modelul matematic al oscilației armonice este:
u (t) = Ums sin (? st +? s) (11)
După cum se poate observa din modelul matematic, spectrul fluctuațiilor unei componente armonice este prezent, care este pe frecvența? S. Înălțimea componentei în amplitudine a spectrului egal cu fluctuațiile de amplitudine UMS, și spectru de fază - faza inițială a oscilației s ?. Mai mult decât atât, construcția spectrului este necesară între semnalul de timp și amplitudinile diagrama spectrului. Amplitudinea componentei spectrului trebuie să corespundă ajustarea amplitudinii vibrațiilor în diagrama de sincronizare.
Trebuie remarcat faptul că prin creșterea frecvenței componentei semnalului va fi îndepărtat de pe axa de frecvență de la zero (Figura 13).
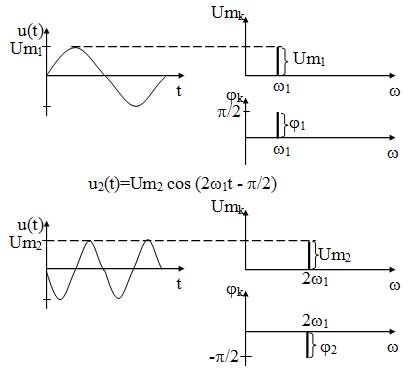
Figura 13 - Reprezentarea spectrală a oscilațiilor armonice
După cum se poate observa din figuri, spectrul oscilații armonice este discret și limitată.
2. periodice, semnalele nearmonice.
Caracteristica principală a reprezentării spectrale a semnalului este prezența unei multitudini de componente spectrale ale spectrului. Aceste semnale pot fi descrise printr-o serie Fourier, conform căreia:
t. e. semnalul poate fi reprezentat de suma componentei constante și o multitudine de componente armonice.
Transformarea seriei folosind proprietatea trigonometrice
sin (x + y) = sin x cos y + cos x păcat y (13)
? Presupunând că x = k și y = k ct obține:
Deoarece UMK și? K sunt parametrii seriei, aceștia pot desemna coeficienți
UMK păcat. k = ak; cos UMK? K = bk (15)
Apoi, seria va fi:
un număr de parametri pot fi definite în termeni de coeficienți ak și bk:
Amplitudinea componentei și coeficienții de CC poate fi determinată prin valoarea semnalului u (t):

Să considerăm reprezentarea spectrală a semnalelor periodice, nearmonice pe un exemplu de o secvență periodică de impulsuri dreptunghiulare (PIP).
Următorii parametri trebuie să fie calculate în cazul în care construcția spectrului:
a) semnal de ciclu:
b) valoarea componentei constante:
c) frecvența primei armonici a spectrului, care este egală cu frecvența semnalului:
g) spectrul amplitudinea componentelor armonice:
În construirea spectrului este necesar de menționat următoarele caracteristici:
1. Toate componentele armonice sunt la frecvențe care sunt multipli ai frecvenței fundamentale (2 1, 3 1, 4 1, etc ??? ...);
2. Pentru intervalele de spectru:
a) are un spectru, STD natura petale, adică în spectrul poate aloca o multitudine de „petale“ ..;
b) numărul componentelor armonice din petalele depinde de ciclul de funcționare și este egal cu q - 1;
c) amplitudinea componentelor armonice, care sunt la frecvențe care sunt multipli ai ciclului de lucru, egal cu zero;
g) forma plicului de spectru este notat - linia punctată care leagă lin nodurile componente armonice;
d) punctul, din care provine plicul este egal sau 2U0 2I0.
3. Pentru faza spectrului:
a) toate componentele armonice la frecvențe care nu sunt multipli ai ciclului de funcționare, sunt de aceeași înălțime egală cu / 2 (90 °) ?;
b) toate componentele armonice într-un singur lob au același semn, iar în opusul vecin.
c) componente la frecvențe multipli ai ciclului de funcționare au o fază inițială egală cu zero.
Sâmburi spectre când q raportul taxei = 3 sunt prezentate în figura 14.
După cum se poate observa din diagramele, spectrul de STD este discret și nelimitat. De aceea, lățimea spectrului pentru a primi intervalul de frecvență, în care primii doi lobi, deoarece în ele conținea aproximativ 95% din energia semnalului ..:
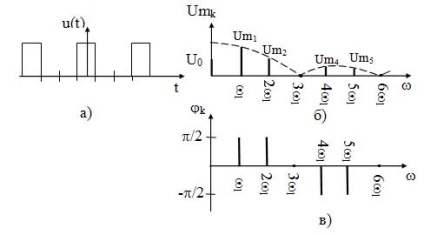
Figura 14 - spectral reprezentare; STD: a) o diagramă de sincronizare; b) diagrama spectrală a amplitudinilor; c) un spectru faze diagramă
După cum se vede din PIP lățime spectrală depinde numai de durata impulsului și este independentă de perioada sa.
3. Semnalele neperiodice.
Deoarece semnalele neperiodice nu se poate selecta perioada t. K. TA să calculeze și să se trasează spectrul prin aceeași metodă ca și că este imposibil pentru semnale periodice. Cu toate acestea, cunoașterea spectrului acestor semnale este necesar, adică. K. Toate semnalele de informație sunt non-periodice. Pentru a construi un spectru semnal nonperiodic produs următoarea procedură: semnal mental ca un lot cu o perioadă arbitrară, care construiesc ddlya spectru. Apoi, procesul de limitare perioada la infinit (?? T) (Figura 15) permițându. Frecvența primei armonici și, în consecință, distanța dintre componentele armonice tind spre zero (f1 = 1 / T), astfel încât toate componentele îmbinare între ele și formează un spectru continuu.
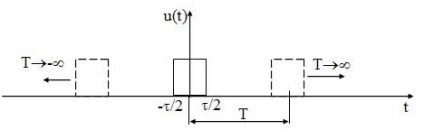
Figura 15 - Semnalul de impuls u (t) și semnalul său de reprezentare periodică
Forma plicului de spectru este notat semnale nonperiodic (linii solide) (Figura 16).
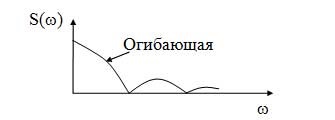
Figura 16 - Semnalul nonperiodic diagramă spectrală
Seria Fourier pentru astfel de semnale, de asemenea, nu pot fi înregistrate, t. K. În acest caz, amplitudinea componentei DC și coeficienții ak și bk sunt zero. În acest caz, valoarea semnalului la un moment dat este, de asemenea, egal cu zero, ceea ce nu este adevărat. Prin urmare, pentru o astfel de utilizare a transformata Fourier a semnalelor:
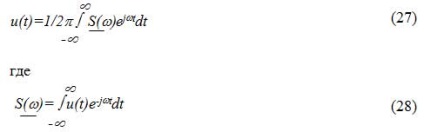
Amploarea S (?) Este densitatea spectrală complexă u semnal (t) este nonperiodic. Acesta este egal cu:
în care amplitudinile densitate spectrală S sau nonperiodic spectrul de amplitudine a semnalului, un (?) (?) - spectru de fază a semnalului nonperiodic.
Densitatea spectrală a amplitudinilor semnalului aperiodice la orice frecvență. egală cu amplitudinea totală este situat într-o bandă mică. frecvența în apropiere. recalculează la 1 Hertz.
diagrame de temporizare și densitate spectrală de amplitudine pentru impulsuri dreptunghiulare și triunghiulare sunt prezentate în Figura 18:
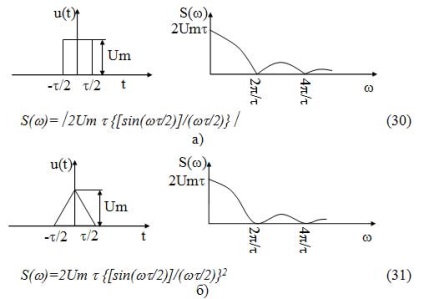
Figura 18 - Reprezentarea spectrală a semnalelor nonperiodic: a) un puls dreptunghiular; b) un impuls triunghiular