Astfel, funcția compozit derivat (z) pentru fiecare variabilă independentă (u și v) este suma produselor din derivatele parțiale ale acestei funcții (z) în variabilele intermediare (x și y) pe derivatele variabilei independente respective (u și v).
În toate cazurile, formula
(Proprietate diferențială invarianță Total).
Decizie. Aplicând formula (4) și (5), obținem:
Exemplu. Arătați că funcția satisface ecuația.
Decizie. Funcția depinde de x și y prin argumentul intermediar. prin urmare
Substituind derivatele parțiale în partea stângă a ecuației, avem:
. t. e. funcției z satisface această ecuație.
Derivatul în această direcție și gradientul
1 °. Funcția derivat în această direcție. Derivata funcției z = f (x, y) în această direcție se numește. în cazul în care - valoarea funcției la punctele și. Dacă funcția z este diferențiabilă, atunci următoarea formulă
unde - unghiul dintre direcția l și axele de coordonate corespunzătoare. Derivata într-o anumită direcție caracterizează rata de schimbare în această direcție funcție.
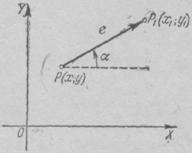
Exemplu. Găsiți derivatul z = 2x 2 - 2 Zu la punctul P (1, 0), într-o direcție care face un unghi cu axa x la 120 °.
Decizie. Noi găsim derivatele parțiale ale acestei funcții, și valorile lor la punctul P:
Aici cos = cos 120º = - ½,
Aplicând formula (1), obținem:
Semnul minus indică faptul că funcția în acest moment, în această direcție se diminuează.
2º. Gradient funcția funktsii.Gradientom z = f (. X y) este un vector ale cărui proiecții pe axele sunt derivatele parțiale corespunzătoare acestei funcții:
Derivata acestei funcții în gradientul l direcție asociată cu formula funcției. t. e. derivatul în această direcție este o funcție de proiecție a gradientului în direcția diferențierii.
Gradientul fiecărui punct este normal la nivelul liniei funcției corespunzătoare. Direcția de o funcție de gradient în acest moment este direcția cea mai mare rată de creștere a funcției, la acel moment, t. E. Când l = derivat z grad are valoarea sa maximă egală.
determinat în mod similar gradientului funcției de trei variabile u = f (x y z ..):