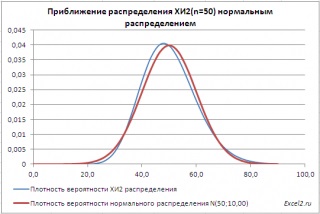
Luați în considerare o distribuție chi-pătrat. Cu funcția MS EXCELHI2.RASP () vom construi grafice ale funcției de distribuție și de probabilitate densitatea, explica utilizarea acestei distribuții pentru statisticile matematice.
Chi pătrat (X 2 Hi2, angl.Chi-squareddistribution) este utilizat în diferite metode de statistică matematică:
Definiția. Dacă x1. x2. ..., xn sunt variabile aleatoare independente distribuite de standardul N distribuție normală (0, 1), distribuția variabilei aleatoare Y = x 1 2 + x 2 2 + ... + x n 2 X 2 are o distribuție cu n grade de libertate.
RaspredelenieH 2 depinde de un parametru, numit gradul de libertate (df, degreesoffreedom). De exemplu, în construcția de intervale de încredere pentru estimarea varianței egal cu numărul de grade de libertate df = n-1, în care n - mărimea eșantionului.
Distribuția densității este exprimată prin formula 2:
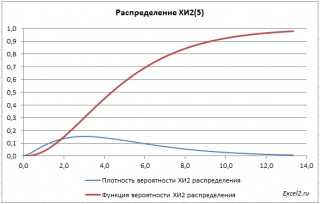
graficele funcțiilor
În fișierul pe foaia din exemplul Graph prezintă grafice ale distribuției densității de probabilitate și funcția de distribuție cumulativă.
proprietate utile Hi2-distribuție
Fie X1. x2. ..., xn sunt variabile aleatoare independente, distribuite în mod normal cu parametrii identici μ și σ, în timp ce XCR este media aritmetică a acestor valori x.
Apoi variabila y este aleatoare
2 are o distribuție X cu n-1 grade de libertate. Folosind definiția expresiei dispersiei eșantionului de mai sus poate fi rescrisă după cum urmează:
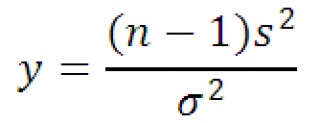
În consecință, statisticile de distribuție selectivă y, atunci când prelevarea de probe dintr-o distribuție normală. X 2 are distribuție cu n-1 grade de libertate.
Această proprietate vom avea nevoie în construcția de intervale de încredere atunci când se evaluează dispersia distribuției. pentru că dispersia poate fi doar un număr pozitiv, iar X 2 de distribuție este utilizat pentru evaluarea sa, apoi db y> 0, așa cum este specificat în definiția.
Hi2-distribution în MS EXCEL
Notă. pentru că Hi2-distribuție este un caz special al distribuției gamma. GAMMA.RASP formula = (x n / 2, 2, TRUE) pentru întreg pozitiv n returnează același rezultat ca formula = HI2.RASP (x; n; TRUE) sau = 1 HI2.RASP.PH ( x; n). GAMMA.RASP formula A = (x n / 2; 2; FALSE) returnează același rezultat ca formula = HI2.RASP (x; n; FALSE). și anume distribuția densității veroyatnostiHI2.
HI2.RASP.PH () funcția returnează funcția de distribuție. mai precis - dreapta-probabilitate, și anume, P. Este clar că egalitatea
HI2.RASP.PH = (x; n) + HI2.RASP (x; n; TRUE) = 1
deoarece primul termen calculează probabilitatea P, iar al doilea P.
HI2.RASP () este singura funcție care returnează densitatea de probabilitate Hi2-distribuției (al treilea argument trebuie să fie setat la FALSE). Funcțiile rămase returnează funcția de distribuție cumulativă. și anume probabilitatea ca o variabilă aleatoare ia valoarea intervalului specificat: P.
Funcțiile de mai sus sunt prezentate în exemplul de fișier MS Excel în funcțiile foii de lucru.
Ne găsim probabilitatea ca variabila aleatoare X are o valoare mai mică sau egală cu un anumit x. P. Acest lucru se poate face în mai multe funcții:
HI2.RASP = (x; n; TRUE)
= 1-HI2.RASP.PH (x; n)
= 1-HI2RASP (x; n)
HI2.RASP.PH () întoarce probabilitatea P, așa-numita dreapta-probabilitate, prin urmare, pentru a găsi P, este necesar să se scade 1 din rezultat.
Să ne găsim probabilitatea ca variabila aleatoare X are o valoare mai mare decât o dată de x. P. Acest lucru se poate face în mai multe funcții:
= 1-HI2.RASP (x; n; TRUE)
HI2.RASP.PH = (x; n)
HI2RASP = (x; n)
Funcția inversă Hi2-distribuire
Funcția inversă este utilizată pentru a calcula quantile alfa. și anume pentru calcularea valorilor x pentru o probabilitate dată alfa. în care x ar trebui să satisfacă expresia P = alfa.
Funcția HI2.OBR () este folosit pentru a calcula intervalele de încredere ale dispersiei unei distribuții normale.
Funcția HI2.OBR.PH () este folosită pentru a calcula chintila superioară. și anume Dacă argumentul funcției este specificat nivelul de semnificație, de exemplu 0,05, funcția returnează o valoare a variabilei x aleatoare astfel încât P = 0,05. Ca HI2.OBR funcție comparație () returnează o valoare a variabilei x aleatoare astfel încât P = 0,05.
Funcțiile de mai sus pot fi interschimbate, ca Următoarele formule returnează același rezultat:
= HI.OBR (alpha; n)
HI2.OBR.PH = (1-alfa; n)
HI2OBR = (1- alfa; n)
Câteva exemple de calcule sunt prezentate în exemplul dosarul funcțiilor foii de lucru.
Funcții MS EXCEL folosind Hi2-distribuție
Cele mai relevante numele de funcții română și engleză:
HI2.RASP.PH () - Ing. numele CHISQ.DIST.RT, și anume CHI-Squared DISTRIBUȚIE Coada dreapta, dreapta-coada Chi-pătrat (d) de distribuție
HI2.OBR () - Ing. numele CHISQ.INV, și anume CHI-Squared Inverse distribuție
HI2.PH.OBR () - Ing. numele CHISQ.INV.RT, și anume distributie CHI-Squared Inverse Coada dreapta
HI2RASP () - Ing. Numele CHIDIST, funcția este CHISQ.DIST.RT echivalentă
HI2OBR () - Ing. numele CHIINV, și anume CHI-Squared Inverse distribuție
Estimarea parametrilor de distribuție
pentru că de obicei, de distribuție Hi2 este utilizat în scopul statisticii matematice (calculul intervalelor de încredere, testarea ipotezelor, etc.), și aproape niciodată pentru a construi modele de valori reale, alocarea pentru această discuție a estimărilor parametrilor de distribuție nu se realizează.
Apropierea Hi2-distribuție a distribuției normale
Dacă numărul de grade de libertate n> 2 X 30 de distribuție este bine aproximată printr-o distribuție normală cu media μ = n și o variație σ = 2 * n (a se vedea. Exemplu foaie imagine Aproximarea).