În cazul în care punctul de aplicare a forței F este situat pe partea de frontieră a kernel-ului, zona de alungire va fi. puterea de a scoate infima din miez va duce la ceea ce va fi zona de întindere, menit să arate linia neutră de bază de delimitare pentru secțiunea noastră.
Prin urmare, pentru a construi kernel-ul trebuie să ia în considerare tot felul de tangentelor la secțiunea și pentru a găsi aceste cazuri, punctul de aplicare a forței. Apoi, conectarea acestor puncte, vom găsi secțiunea miezului.
În cazul în care conturul este format din segmente de linie dreaptă, sarcina de bază de construcție mult mai ușor.
Luați în considerare secțiunea de nucleu procedura de construcție.
Ecuația liniei neutre I-lea (ris.19.15). Această ecuație care trece prin cele două puncte 1-2:
Ecuația (19.9) trebuie să coincidă cu ecuația (19.8). Astfel, ecuația (19.9) este cunoscută, și cunoscut. trebuie să fie găsit.
Pentru aceasta presupunem mai întâi x = 0. Din relațiile (19.9), găsim y. înlocui aceste x, y în ecuația (19.8) și pentru a găsi uF.
Pentru constatare sugerează XF y = 0. Din formula (19.9) găsi x, înlocuim aceste x și y în ecuația (19.8) și pentru a găsi XF.
Notă importantă. Luați în considerare un punct de colț B. După punctul B puteți petrece un număr infinit de tangenta.
Cu toate acestea, toate liniile care trec prin punctul B. descrisă de ecuația, care este satisfăcută prin substituirea. Substitut-le în ecuația (19.8):
Deoarece. - un număr de bine-cunoscut, rezultatul este un
unde a, b, c - constante. Aceasta este ecuația liniei. pe care punctele de granița nucleare.
Astfel, atunci când merge dintr-o parte în alta BC BD. Nu aveți nevoie să caute, și ai nevoie doar pentru a conecta două puncte de o margine dreaptă a nucleului, care sunt obținute pentru BC și BD.
Luați în considerare exemple. Vom găsi secțiunea miezului dreptunghiului.
I-lea linia neutră a ecuației (19.9) are forma:
Apoi, (19.8) ia forma:
Înmulțind de obținem:
Noi credem prima x = 0. Apoi, de la (19.10) rezultă că. Substituind în (19.11), obținem:
Găsim XF. Din moment ce (19.10) poate doar presupune. apoi ne-am stabilit. x - orice număr, de exemplu x = b / 2. Substituind în (19.11), găsim:
La fel găsim o graniță punct în secțiune a nucleului, în cazul în care linia neutră se extinde (linia neutră II-lea) vertical apoi obține. .
In mod similar, un alt 2 puncte sunt determinate. Rezultatul este o secțiune transversală a miezului ilustrat în figura (19,16), sub forma unui romb.
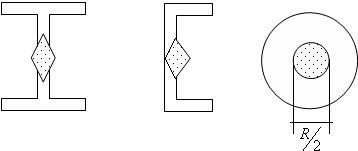
Pentru un fascicul I, canale, nuclei secțiuni gama au tipuri în (ris.19.17).
În unele cazuri, construirea de forțe de impact de construcție care se schimbă rapid în timp. Acest lucru poate duce la două consecințe periculoase:
1) Efectele dinamice pot depăși efectul static al forțelor externe și uneori chiar sute de ori.
2) S-ar putea fi un fenomen de rezonanță.
Există 2 modalități de rezolvare a problemei de determinare a efectelor dinamice asupra structurii organelor. Acestea se bazează, respectiv pe următoarele două legi: legea de conservare a energiei și principiul D'Alembert.
Luați în considerare problema căderii de greutate a sarcinii F = mg cu înălțimea H (sm.ris.20.1).
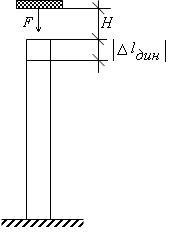
Designer interesat de forța maximă de impact, pe care o numim forța de impact. Alături de această problemă, ia în considerare o problemă fictivă, atunci când forța tijei. care este egală cu greutatea corporală a F.
Forța notată grevă. Este clar că :.
Introducem factor dinamic:
Apoi, tensiunea dinamică va
Conform (1.20), obținem:
Astfel, problema se reduce la calcularea numărului. Pentru ao defini, utilizați legea conservării energiei.
Falling Georgia a comis ceva de lucru. Acest lucru nu poate dispărea, este transformată în energie de deformare tijei comprimat.
Notăm: - forța de lucru F; - energia de deformare a tijei. atunci
În primul rând, vom calcula W:
Aici - o cale care va avea forța F. De la ris.20.1 este clar că:
Calculăm energia de deformare a tijei:
Substituind legea de conservare a energiei (20,4), obținem:
Reducerea pentru a obține o ecuație pătratică pentru:
Solutia sa are forma:
Aceasta este formula de bază pentru calcularea factorului dinamic. În cazul în care H - înălțimea de cădere de transport maritim;
- tija de manechin pentru problema de deformare sub sarcină statică (ris.20.2)
1) Chiar dacă înălțimea de cădere H = 0, în conformitate cu (20.5), forța de încărcare bruscă dublează greutatea încărcăturii.
2) mai mare (adică, mai tijă precipitat), cu atât mai puțin efectele adverse ale impactului, deoarece devine mai mică. Din legea lui Hooke, rezultă că acest lucru poate fi realizat prin 3 metode:
1. Creșterea lungimii tijei
2. Decrease grosime tijă
3. Scade rigiditatea (E) a tijei
Notă: formula (20,5), poate fi aplicat cu impactul asupra grinzii (ris.20.3). În acest caz, aveți nevoie pentru a înțelege o deformare (sm.ris.20.3):