O linie dreaptă obținută prin intersecția reciprocă a celor două planuri, aceasta este definită prin două puncte, fiecare aparținând ambelor planuri. Astfel, linia K1 K2 (Fig. 163), pe care se intersectează planul definit prin triunghiul ABC și pl. β, o linie dreaptă predeterminată DE și DF, trece prin punctul K1 și K2; dar la aceste puncte liniile drepte AB și AC intersectează primul plan Sq. β t. e. K1 și K2 punct aparțin ambelor avioane.
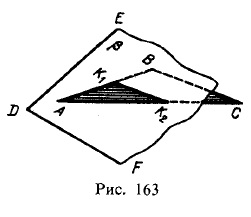
Prin urmare, în general, pentru a construi linia de intersecție a două avioane trebuie să găsească oricare două puncte fiecare aparținând ambelor planuri; Aceste puncte definesc linia de intersecție a avionului.
Pentru a găsi fiecare dintre aceste două puncte este de obicei necesară pentru a efectua construcții speciale. Dar, dacă cel puțin unul dintre avioanele care se intersectează perpendicular pe planul de proiecție, construcția liniei de intersecție a proiecțiilor este simplificată. Să începem cu acest caz.
Fig. 164 arată intersecția a două plane, dintre care unul (dat triunghi DEF) este perpendicular pe pl. π2. Deoarece triunghiul DEF pl.π2 proiectat pe o linie dreaptă (D „F“), vedere frontală a segmentului de linie pe care se intersectează ambele triunghiuri reprezintă intervalul R „1 R“ 2 proiecție D „F“. Mai departe de construcție este clar din desen.

Un alt exemplu este prezentat în Fig. 165. orizontal proeminente plane subunitatea intersectează planul triunghiului ABC. Proiecția orizontală a liniei de intersecție a acestor avioane - segment M'N „- este determinat pe pista α“.
Acum, ia în considerare cazul general de a construi linia de intersecție a două avioane. Să unul din avioane, beta, definit de două linii care se intersectează, iar celelalte, y, - două linii paralele. Construcția prezentată în Fig. 166. Ca urmare a intersecției reciproce a p plane și γ linia obținută K1 K2. Pentru a exprima această înregistrare: β × γ = K1 K2.
Pentru a determina pozițiile punctelor K1 și K2 ia două auxiliare frontale plane de proiecție (α1. Și α2), planurile care se intersectează fiecare β și γ. La intersecția planelor p și α1 γ plan. Vom ajunge direct la proiecțiile de 1 "2", 1/2 "și 3", 4“, 3'4' . Aceste linii sunt situate în Piața. α1. în intersecția defini primul punct K1. linia de intersecție a avioanelor p și γ.
Prin introducerea il continuare. α2. Obținem la intersecția cu p și y direct cu proeminențele 5 „6“, 5'6 „și 7“ 8“, 7'8' . Aceste linii sunt situate în Piața. α2. în intersecția lor determină al doilea punct, K2. comune p și y.
Primirea K'1 proiecție și k'2 este pe cale și α 2 proiecție "1 și a" K '1 și K' 2. Aceasta determină k'2 proiecția K'1 și R „1 R“ 2 a liniei dorite de intersecție a β plane și γ (proiecția realizată linie lanț punct).
Când construirea vă păstrați în minte următoarele: deoarece planul auxiliar intersectându α1 și α2 sunt paralele între ele, prin construirea de proiecție 1'2 „și 3'4“ ar trebui să fie pentru proiecțiile 5'6 „și 7'8“ să-și asume un punct, deși la 5 și 8, ca 5'6 '|| 1'2' și 7'8 '|| 3'4'.
În construcția de mai sus au fost luate ca auxiliar frongalno- două plane proeminente. Desigur, puteți lua avionul și celălalt, de exemplu, două orizontale sau una orizontală și cealaltă față, și așa mai departe. D. Esența construcțiilor nu se schimbă. Cu toate acestea, ea poate îndeplini acest caz. Să presupunem că au fost luate ca două plane auxiliare orizontale obținute la trecerea
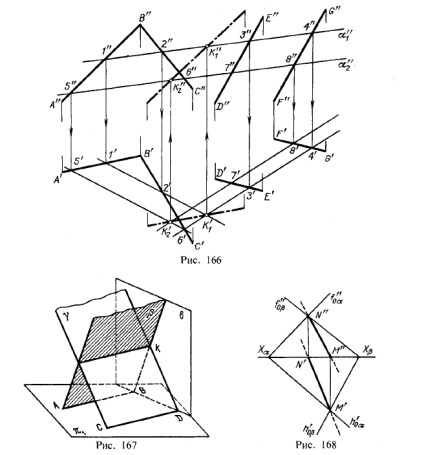
plane p și γ orizontal avansat paralele reciproc. Dar Fig. 167 arată că p și y se intersectează reciproc, deși ele sunt paralele cu orizontala. Prin urmare, având proeminențe orizontale paralele între ele de contururi AB și CD, și știind că avionul nu este paralelă în mod necesar, și se pot suprapune (la orizontală lor comună), este necesară testarea p plane și y, folosind cel puțin, plane proeminent gorizongalno (vezi . Figura 167) .; în cazul în care liniile pe care acest plan auxiliar sigma, p, și y se intersecteaza, de asemenea, s-ar fi transformat în paralel una față de alta, p plane și y nu se intersectează și sunt paralele una față de cealaltă. Fig. 167 din aceste linii se intersectează în punctul K și prin care trece intersecția planelor β și y de linii paralele BA și CD-uri.
În cazul în care planurile sunt definite acestea ar trebui să fie pe planul de proiecție, este firesc să caute punctele care definesc linia de intersecție a avionului la punctele de intersecție ale planului următor același nume (Figura 168.): O linie dreaptă care trece prin aceste puncte, este comun pentru ambele planuri, și anume, linia lor .. intersecție.
O schemă pentru construirea intersecția celor două planuri ale liniei (vezi. Fig. 166) pot, desigur, să fie extins la cazul stabilirii planurilor de piste lor. Aici rolul avionului secțiunii auxiliare se executa planul de proiecție:
Punctele de intersecție ale planului următor același nume sunt urme linia de intersecție a acestor avioane. Prin urmare, pentru a construi linii de proiecție de intersecție ale avioanelor a și p, este necesar (Figura 168.): 1) pentru a găsi un punct M „la intersecția urmelor și h'0α h'0β
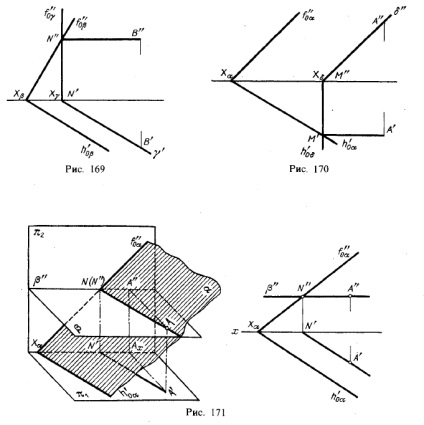
și punctul N „la intersecția f“ 0α și f „0β și pe ele - proiecția M.“ și N „; 2) să dețină o linie dreaptă M „N“ și M'N“,
Fig. 169-171 arată atunci când știi direcția liniei de intersecție. Prin urmare, este suficient pentru a avea un punct lysh de la intersecția ar trebui să continue să dețină linia care trece prin acest punct, în funcție de poziția avionului și urmele lor.
Întrebări pentru §§ 22-24
- Care este poziția relativă a celor două avioane pot lua?
- Care este semnul paralelism a două avioane?
- Ca urmele roților sunt aranjate reciproc paralele unul cu celălalt plan cu două proeminente frontal?
- Ca aranjate reciproc două trasee paralele orizontale între un plan orizontal proeminent?
- Ca urmele de același nume aranjate reciproc două planuri reciproc paralele?
- Servește ca un semn dacă intersecția reciprocă a celor două planuri care traversează cel puțin o pereche de piese de același nume?
- Cum de a stabili poziția relativă a liniilor și avioane?
- Cum este o linie dreaptă cu punctul de intersecție al unui plan perpendicular pe una sau două planuri de proiecție?
- Care punct de numere aranjate în general perpendicular pe o) mp. π1 b) pl. π2 considerate vizibile respectiv pe π1. pe π2?
- Cum este linia de intersecție a două planuri, dintre care cel puțin unul este perpendicular pe pătrat. π1 sau pl. π2?
- Care este metoda generală pentru construirea liniei de intersecție a două avioane?