Termenul "energie" a fost introdus în 1807 de către omul de știință englez T. Jung. În greacă, acest cuvânt înseamnă În general, corpul are atât energie cinetică, cât și potențială. Suma lor se numește energie mecanică totală:
E = Ek + En (15,1)
Acest concept a fost introdus în 1847 de către savantul german H. Helmholtz de 26 de ani.
Ce se întâmplă cu energia mecanică totală pe măsură ce corpul se mișcă? Pentru a afla acest lucru, ia în considerare un fenomen simplu.
Aruncă mingea vertical. Dând viteza mingii. îl informăm astfel despre o anumită energie cinetică. Pe măsură ce muta mingea în sus mișcarea lui va încetini rata de atracție a Pământului și, împreună cu ea, iar energia cinetică a mingea va deveni mai mici și mai mici. Energia potențială a mingii, împreună cu înălțimea k, va crește apoi. Cel mai înalt punct al traiectoriei (la înălțimea maximă), energia potențială a balonului atinge valoarea sa maximă, iar energia cinetică va fi egală cu zero. După aceasta, mingea va începe să coboare, câștigând treptat viteza. Energia cinetică va crește apoi, iar energia potențială (datorată scăderii altitudinii) va scădea. În momentul impactului cu energia cinetică la sol a balonului atinge valoarea maximă, și dispare energia potențială.
Deci, atunci când energia cinetică a corpului scade, energia potențială crește și viceversa, atunci când crește energia cinetică a corpului, energia sa potențială scade. Studiul căderii libere a corpului (în absența rezistenței la aer) arată că orice scădere a unuia dintre aceste tipuri de energie este însoțită de o creștere egală a celuilalt tip de energie. În același timp, energia mecanică totală a corpului rămâne. Aceasta este legea conservării energiei mecanice:
Energia mecanică totală a corpului, care nu este acționată de forțele de frecare și rezistență, rămâne neschimbată în timpul mișcării sale.
Dacă denotăm energiile inițiale și finale ale corpului cu E și E ', atunci legea conservării energiei poate fi exprimată sub forma următoarei ecuații:
E = E '(15,2)
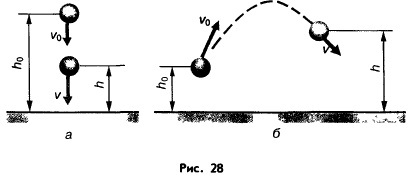
Să presupunem că un corp în mișcare liberă în momentul inițial al timpului era la o înălțime h0 și avea o viteză V0 în același timp. Apoi, energia sa mecanică totală în această clipă era egală cu:
Dacă, după un timp, corpul luat în considerare este la înălțimea h, având o viteză V (Figura 28), atunci energia mecanică totală va fi egală cu:
Conform legii conservării energiei, ambele valori ale energiei trebuie să coincidă. prin urmare
În cazul în care inițial H0 valorile și cunoscute, această ecuație vă permite să găsiți viteza corpului V la o înălțime h, sau, invers, h înălțimea la care organismul va avea o V. viteză predeterminată Greutatea corporală, în același timp, nici un rol nu va, ca în ecuația (15.5 ) se micșorează.
Trebuie reținut faptul că energia mecanică totală este reținută numai atunci când nu există forțe de frecare și rezistență. Dacă aceste forțe sunt prezente, atunci acțiunea lor duce la o scădere a energiei mecanice.
. 1. Ce se numește energie mecanică totală? 2. Formulează legea conservării energiei mecanice. 3. Cu ce energie - cinetică sau potențial - energia mecanică totală a unui corp care cădea liber coincide în momentul impactului asupra pământului? 4. Cu ce energie face energia mecanică totală a unei minge învârtată vertical coincide în momentul în care se află la cel mai înalt punct al zborului? 5. Ce se întâmplă cu energia mecanică totală a corpului în prezența forțelor de frecare și de rezistență?
SV Gromov, N.A. Patriei, clasa fizică 8
Cititorii au trimis de pe site-uri web
Publicațiile electronice sunt gratuite, bibliotecă de fizică, lecții de fizică. program cu fizica, rezumate de lecții de fizică, manuale de fizică, teme pregătite
Dacă aveți corecții sau sugestii pentru această lecție, scrieți-ne.
Dacă doriți să vedeți alte ajustări și dorințe pentru lecții, consultați aici - Forumul educațional.