Asix Admin. a raspuns acum 8 luni
Cercul inscripționat într-un trapez isoscel reprezintă câteva trăsături ale acestui trapez.
Luați în considerare.
- Un cerc într-un trapez poate fi înscris numai în cazul în care sumele perechilor de fețe opuse sunt aceleași.
Cu alte cuvinte, cercul din trapezoid poate fi înscris când:
AB + CD = AD + BC.
Reversul este de asemenea adevărat:
Dacă sumele perechilor perechi opuse ale trapezoidelor sunt aceleași, atunci un cerc poate fi înscris într-un astfel de trapez.
Din toate cele de mai sus rezultă că dacă trapezoidul este isoscel, atunci:
- Prin proprietatea liniei mediane, dacă un cerc poate fi înscris într-un trapez isoscel, atunci laturile sale sunt lungimea liniei mediane.
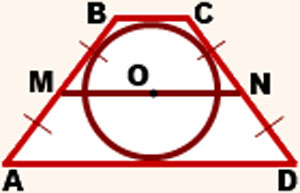
- Înălțimea unui trapez izoscel poate fi exprimată prin bazele acestui trapez.
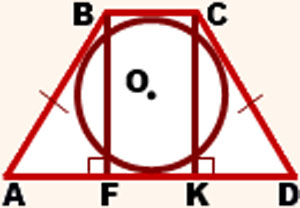
Conform uneia dintre proprietățile unui trapez izoscel, scriem:
Partea acestui trapez este:
Luați în considerare triunghiul drept ABF.
Prin teorema lui Pythagoras, scriem: