1. Legătura dintre energia potențială și puterea. Energia potențială a gravitației și a deformărilor elastice.
Spațiul în care operează forțele conservatoare se numește câmpul potențial. La fiecare punct al câmpului potențial corespunde o anumită valoare a forței F care acționează asupra corpului și a unei anumite valori a energiei potențiale U. Prin urmare, trebuie să existe o legătură între forța F și U. pe de altă parte, dA = -dU, prin urmare Fdr = -dU, prin urmare:
Proiecțiile vectorului de forță pe axa de coordonate:
Vectorul de forță poate fi scris în termenii proiecțiilor :, F = -grad U, unde.
Un gradient este un vector care arată direcția celei mai rapide modificări a funcției. Prin urmare, vectorul este direcționat către cea mai rapidă scădere a U.
Energia potențială a deformării elastice (arcuri)
Vom găsi munca efectuată când arcul elastic este deformat.
Forța elastică Fupr = -kx, unde k este coeficientul de elasticitate. Forța nu este constantă, deci munca elementară dA = Fdx = -kxdx.
(Semnul minus spune că lucrarea se face în primăvară). Apoi, adică A = U1 - U2. Luăm: U2 = 0, U = U1, atunci.
În Fig. 5.5 prezintă o diagramă a energiei potențiale a arcului.
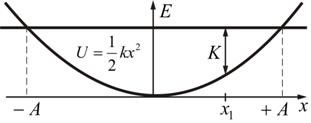
Fig. 5.5
Aici, E = K + U este energia mecanică totală a sistemului și K este energia cinetică în punctul x1.
Energie potențială pentru interacțiunea gravitațională
Lucrarea corpului la cădere A = mgh, sau A = U - U0.
Am acceptat să presupunem că pe suprafața Pământului h = 0, U0 = 0. Atunci A = U, adică A = mgh.
Pentru cazul interacțiunii gravitaționale dintre masele M și m, situate la o distanță r una de cealaltă, energia potențială poate fi găsită prin formula.
În Fig. 5.4 prezintă o diagramă a energiei potențiale a atracției gravitaționale a maselor M și m.
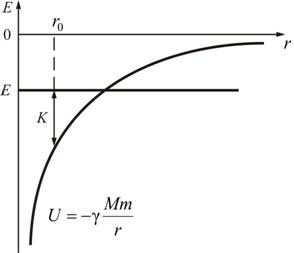
Fig. 5.4
Aici, energia totală este E = K + E. De aici este ușor să găsim energia cinetică: K = E - U.

3. La ce viteză se deplasează particula dacă energia sa totală este de două ori restul energiei?

4. Volumul molii unui gaz ideal cu un exponent adiabatic γ variază în conformitate cu legea V = a / T, unde a este o constantă. Găsiți cantitatea de căldură produsă de gaz în acest proces dacă temperatura sa sa modificat cu δT.
