(3 voturi, medie 4.33 din 5)
Funcția y = f (x) este numită chiar. dacă
• domeniul de definire a acestei funcții este simetric față de punctul O, adică și D (f) dacă τ -a D (f), atunci τ.
• Pentru orice valoare a lui x D (f), egalitatea f (x) = f (- x) este valabilă.
Funcția y = f (x) se spune a fi ciudată. dacă
• domeniul de definire al acestei funcții este simetric în punctul O;
• Pentru orice valoare a lui x D (f), egalitatea f (-x) = -f (x) este valabilă.
Diagrama unei funcții uniforme este simetrică în raport cu axa de coordonate (vezi figura 1).
Figura 1
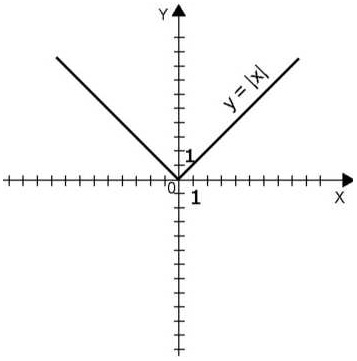
Graficul funcției impare este simetric în raport cu m (0; 0) (vezi figura 2).
Figura 2
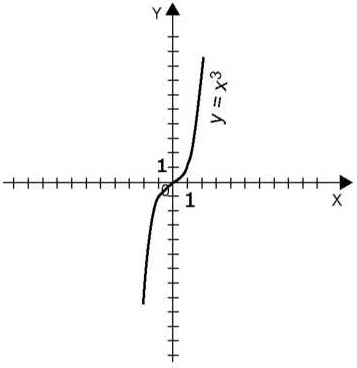
Există funcții care nu sunt ciudate sau ciudate.
Funcția y = f (x) se spune că este periodică. dacă există un număr T> 0. că pentru fiecare x în domeniul definirii acestei funcții valorile x + T și x-T aparțin, de asemenea, domeniului definiției și egalității f (x + T) = f (x). Numărul T este numit perioada funcției y = f (x). Rețineți că fiecare dintre numerele nT (n = 1, 2, 3, ...) este, de asemenea, o perioadă a funcției y = f (x).
Dacă între perioadele pozitive ale funcției există cel mai mic număr, atunci se numește cea mai mică perioadă pozitivă.
Periodic, de exemplu, sunt funcțiile trigonometrice y = sinx, y = cosx, y = tgx, y = ctgx.
În Fig. Figurile 3 și 4 prezintă graficele funcțiilor cu secțiunile selectate corespunzând celor mai mici perioade pozitive ale acestor funcții.
Figura 3
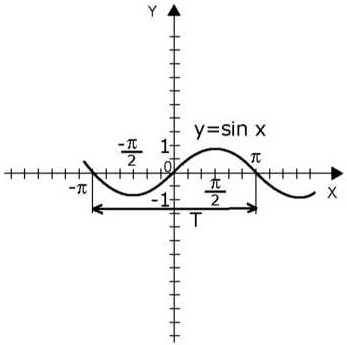
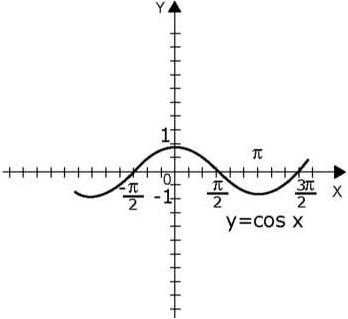
Un exemplu. Dovedeste ca functia f (x) = | sin sin x | este periodic cu perioada π.
D (f) = R, prin urmare pentru orice x punctele x + π și x-π aparțin domeniului definiției.
Pentru a construi un grafic al unei funcții periodice cu perioada T este suficient să construim pe un interval de lungime T și apoi să transferăm graficul rezultat în paralel cu distanțele nT spre dreapta și spre stânga de-a lungul axei Ox (nN).
Dacă funcția f (x) are o perioadă T, atunci funcția f (ax + b), unde a și b sunt numere arbitrare și a ≠ 0, are o perioadă egală cu T / a.