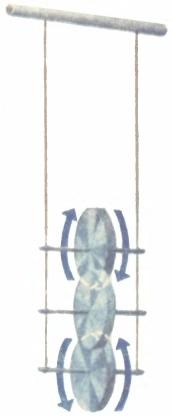
Uită-te la imaginea acestui pendul. Acest disc este montat pe axul la care sunt atașate cele două componente. capetele lor superioare sunt fixate pe bara transversală. Strângeți firul în jurul unei axe - unitate se ridică. Acum eliberați pendulul - și el începe să facă mișcare periodică: primul disc este coborât, firul este derulată, discul se rotește mai repede; atingând punctul cel mai jos și continuă să se rotească prin inerție, unitatea își schimbă direcția de mișcare și se ridică. Deci, pendulează până se oprește.
Câteva sfaturi pentru a face disc pendul trebuie să fie ($ m> $ 100 g), un ($ d> $ 5 cm) axa mare si grea - un strat subțire și ușor, firul - durabil și suficient de lung ($ $ 0.5 m). Este mai bine să aibă un set de unități, am fost pe axa.
Este ușor să dau seama că perioada de oscilație a pendulului, adică. E. Timpul total de coborâre și urcare, nu depinde de masa discului, și depinde de raza sa, iar această dependență este aproape direct proporțională. Acest lucru indică faptul că este necesar să se utilizeze un astfel de lucru ca momentul de inerție J $ $ (disc $ J = mr ^ 2/2 $) pentru a descrie mișcarea unui pendul.
Formula exactă pentru perioada pendulului Maxwell poate fi obținut prin calcule relativ simple (vezi. De exemplu, „Quantum“ Journal 1981, №11).
unde $ l $ - lungimea filamentului, $ r $ - axa raza discului, $ J $ - moment de inerție.
Această formulă poate fi aplicată pe disc, și pentru o sferă, respectiv, prin schimbarea structurii pendulului.