În acest post, vom construi în cele din urmă un grafic al rezultatelor unui studiu anterior.
Într-o serie de posturi dedicate punerii în aplicare a funcțiilor de bază ale unui studiu de design variabil folosind Wolfram | Alpha, ne-am ținut în mod constant o serie de etape, care acționează ca și cum am fi efectuat un studiu al funcției „de mână“. Wolfram | Alfa în același timp, am folosit ca un instrument auxiliar - un fel de calculator pentru toate ocaziile. Acest lucru ne-a permis să scape în mare parte din calculele de rutină și să se concentreze asupra funcției corespunzătoare a studiului. Fără Wolfram | Alpha unele dintre calculele necesare ar fi prea consumatoare de timp pentru calcule de mână și studiul acestei funcții ar părea să ne prea dificil.
Este această filozofie - posibilitatea, în ciuda volumului și complexității calculelor de rutină pentru a investiga oricare dintre funcțiile - principalul motiv în favoarea utilizării Wolfram | Alpha în rezolvarea unor astfel de probleme. De fapt, fără pierderi de generalitate rezolvate sarcini în primul rând metodic - pentru a studia și de a învăța cum să pună în practică schema generală a funcției de cercetare.
Cu toate acestea, în practică, soluția problemelor aplicate, este puțin probabil ca cineva ar merge la un astfel de mod complex și confuz, cu excepția cazului în care există alte posibilități. Și ei sunt. În cursul rezolvării acestor oportunități am examinat sistematic, și a încercat să se concentreze asupra lor atenția: este specifică are nevoie de Wolfram | Alfa, care permite „un singur clic“, după cum este necesar pentru a găsi toate proprietățile individuale și punctele caracteristice ale funcției. O prezentare detaliată a „hands-on“ abordare a studiului funcțiilor cu ajutorul Wolfram | Alpha, în contrast cu „teoretic“, pe care le-am urmărit tot timpul, vor fi prezentate într-unul dintre aceste posturi.
Cu toate acestea, înapoi la etapa finală a schemei clasice a funcțiilor generale de cercetare. Aceasta este a patra etapă în schema generală a funcției de cercetare. Scopul acestui pas - să se bazeze pe rezultatele studiului Graficul de mai sus a funcției:
Sarcina principală a etapei a patra sunt după cum urmează: spolzuya și rezultatele cercetărilor anterioare pentru a construi un grafic al funcției f (x). Pentru aceasta avem nevoie de rezultatele tuturor etapelor anterioare ale funcției de cercetare.
Această sarcină, mai ales pentru activitatea independentă a studenților, necesită precizări în formă de sarcini individuale:
16.1. Egal sistem de coordonate, având în vedere rezultatele anterior domeniului acestei funcții (. Vezi, de asemenea, domeniul de funcție în Wolfram | Alpha) și o multitudine de valori ale acestei funcții (a se vedea, de asemenea: o multitudine de valori funcționale în Wolfram | Alpha.). Aceste informații sunt necesare în această etapă pentru a atrage sistemul de coordonate, astfel încât graficul funcției este situat în scara mare și în centru, și nu ca un „cocoș foarte singuratic“ în cartea de ochi-de deschidere a copilului despre Carlson, care trăiește pe acoperis :)
16.2. Marcați punctul de pe axa x a discontinuității. Informații cu privire la punctele de discontinuitate sunt obținute în domeniul de investigare a acestei funcții.
16.9. Desenați grafic funcție cu toate semnele și puncte, aplicate la desen. Nu am făcut acest lucru aici - pur și simplu prea leneș pentru a face acest lucru manual (desena grafic pe hârtie și apoi fotografia sau scanare.). Cu atât mai mult în secțiunea următoare, am primit deja acest program folosind Wolfram | Alpha.
17. Verificați vizual corectitudinea funcțiilor comploteaza utilizați interogarea: complot f (x) x = a..b, unde [a, b] segmentul care conține toate caracteristicile punctelor caracteristice găsite anterior:
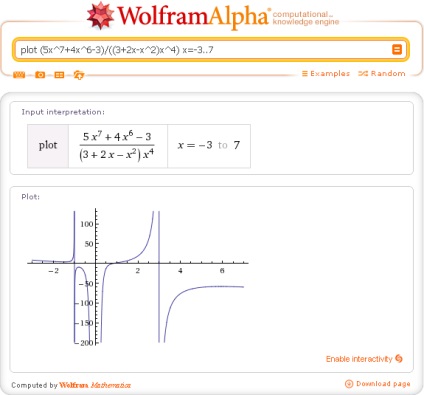
Sau cerere asimptote f (x). că aici, la fel ca în multe alte cazuri, se afișează un rezultat mai evident:
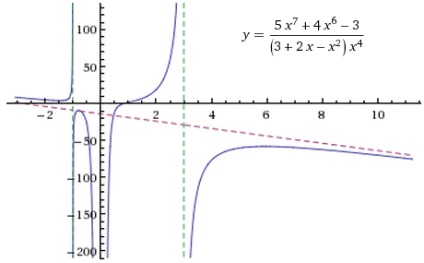
18. Restul, obținută utilizând funcția calendar, analiza proprietățile geometrice ale graficului construit (simetrie în raport cu axa ordonatelor și originea sistemului de coordonate, etc.), și pentru a trage concluzii cu privire la proprietățile chiar impar și periodicitatea funcției f (x). Această parte vă las pentru studiu independent.
P.S.
Așa cum am promis la începutul acestui post, într-unul dintre aceste posturi vor fi furnizate cu o declarație detaliată a „hands-on“ abordare a studiului funcțiilor cu ajutorul Wolfram | Alpha, în contrast cu „teoretic“, pe care le-am urmărit tot timpul.