La disciplina „Computer
Soluție de ecuații diferențiale ordinare. Metoda lui Euler
ecuații diferențiale ordinare se găsesc destul de des în diverse aplicații. Aceste sarcini sunt descrise mișcarea de sisteme de puncte, circuite electrice și altele.
Chemat o ecuație diferențială care se referă variabila independentă X, funcția y său = f (x) și derivații acestei funcții.
În ecuație diferențială implicită este scrisă ca:
Ordinea cea mai derivata, o parte a acestei ecuații se numește ordinul ecuației diferențiale.
Dacă y = f (x) - o funcție a variabilei X independent, o ecuație diferențială ordinară se numește, dacă y = f (x1, x2, ... xn) - o funcție de n variabile independente x1, x2, ... xn. atunci ecuația se numește ecuație diferențială parțială.
Soluția unei ecuații diferențiale ordinare reduce la funcția de surf y = f (x), care, atunci când este substituită în ecuația atrage într-o identitate.
Găsirea unei soluții a unei astfel de ecuație se numește integrarea sa, iar soluția rezultată - integrală a acestei ecuații.
Există soluții generale și particulare ale ecuației diferențiale.
Soluția generală a ecuațiilor este o funcție y = # 966; (x, c), care satisface ecuația pentru orice valoare constantă C.
Soluția particulară este determinată de o valoare deosebită C. Pentru a găsi o anumită soluție trebuie să specifice condițiile inițiale, și anume, setați valoarea y, dacă x = x0. și anume y0 = y (x0), ...,
Sarcina de a găsi o soluție la o ecuație diferențială obișnuit cu condițiile inițiale se numește problema Cauchy pentru ecuații diferențiale ordinare.
Considerăm ecuația rezolvată pentru cea mai mare derivata.
Ele pot fi reduse la un sistem de n ecuații diferențiale ordinare de ordinul întâi pentru înlocuirea funcției necunoscute P1 (x), P2 (x), etc. și anume
Mai mult decât atât, condițiile inițiale:
Pentru soluția, vom lua în considerare metodele Euler si Runge-Kutta.
Soluție numerică este de a construi un tabel de valori aproximative y1, y2, ..., yn-1 exactă soluții y (x) ecuație.
Noi nu știm tipul de funcție, nu putem calcula direct valoarea funcției. știu doar condițiile inițiale, valorile X0 = a, y0 = y (x0) și intervalul [a, b] funcția, care este necesar să se integreze.
Problema este formulată după cum urmează: punctele X0, X1, ..., Xn pentru a găsi aproximările y0, y1, ..., yn de soluție exactă.
Primul pas - pauză intervalul într-un număr finit de puncte de grila (puncte de rețea). spațiere grilă h = (b-a) / n, Xi = a + ih, I = 0,1. N.
Este necesară pentru a restabili valorile funcției necunoscute. Luați în considerare ecuația diferențială 1-comandă
Al doilea pas - cunoașterea condițiilor inițiale vom calcula valoarea primei derivate de la punctul X0.
Al treilea pas - punctul următor grila calculează valoarea funcției.
A patra etapă se repetă toate.
Metoda de interpretare geometrică constă în înlocuirea curbei integral pe un segment tangențial la punctul xi, yi. La fiecare pas, din nou, determinat de tangenta, și, prin urmare, soluția aproximativă a curbei corespunzătoare este o linie întreruptă. Prin urmare, metoda este, de asemenea, numit prin linii întrerupte.
Schema de calcul: xi = a + ih (I = 0,1, ..., N)
Ie având punctul cunoscut, se calculează după cum urmează. Această schemă de calcul pentru ecuația 1 ordine.
Metoda lui Euler pentru ecuațiile de ordinul 2 este ecuația necesară cu condițiile inițiale reduc la un sistem de două ecuații de ordinul 1:
Derivatele luate la punctul x.
Formula de calcul Iterativa:
În practică, calculele sunt efectuate de jos în sus evaluate inițial 1 derivat, adică pi. și apoi un al doilea Yi.
Pentru ecuația de ordinul doi trebuie aplicată integrarea de două ori. Restabilirea valorii derivatului, iar apoi valoarea funcției dorite, adică, Rezolvăm prima o ecuație, iar apoi a doua.
Exemplu. Pe intervalul [a, b] a crea un tabel de valori ale soluției aproximativă a ecuației diferențiale. satisface condițiile inițiale
Y (0) = 1, Y # 900; (0) = 2. integrare pas h = 0,2, precizie # 949 = 0,001. Pentru a oferi soluții corecte de imprimare valori y = e x + x.
NEVOIE DE matrice X - X din valorile 0 la 2
I - o serie de soluții aproximative
F - o matrice de valori derivate
(A-b) / h + punct inițial = 2 / 0,2 = 10 + 1 = 11
Metoda Euler a considerat se referă la un grup de metode cu un pas. în care pentru calcularea punctului (xi + 1. yi + 1), este nevoie de informații cu privire la ultimul punct de calcul (xi. yi).
Soluția numerică este de a construi un tabel de valori aproximative y1. y2. Y3. ..., yn-1 soluții exacte y (x) ecuația y ¢ = f (x, y), a £ x £ b pentru condiția inițială y (x0) = y0. x0 = o secvență selectată de puncte pe xi = x0 + ih. Funcția y depinde de argumentul x
Eroarea de acuratețea sau de terminare a apelurilor de eroare, ceea ce face trecerea de la precedenta la următoarea X dacă ecuația diferențială se înlocuiește cu membrul de expresie.
Eroarea de aproximare egală cu ecuațiile de diferență eliminată termenul rest al seriei Taylor O (h p + 1).
Se consideră, în cazul în care metoda numerică a formulelor de calcul sunt în concordanță cu o serie de expansiune Taylor, în termeni de ordine h p. numărul p se numește ordinea de precizie a metodei.
În metoda de calcul formula comparația Euler cu extinderea Taylor este consecventă primul ordin de h, adică, Metoda include o primă comandă de precizie cu eroarea O locală (h 2)
Pentru metoda de eroare a lui Euler este 2 h.
10.2. Metode numerice de diagrame
În rezolvarea problemelor pe calculatoare este esențială vizibilitatea și ușurința percepției rapide a fenomenelor studiate. După modul grafic de plată Turbo Pascal este posibil să se construiască diagrame, precum și a primi o varietate de forme geometrice. Oricare ar fi imaginea nu este afișată, acestea sunt construite din puncte, grupul care, la rândul lor, formează segmentele și curbe. Procedura punct de ieșire făcut PutPixel (X, Y, Color), în care X și Y coordonatele ecranului, unde se află punctul. Culoare - culoarea.
Pentru a construi graficul funcției urmați această procedură:
1) Funcția Totalizarea;
2) Determinarea valorilor maxime și minime ale funcției;
3) Formarea și grafică de ieșire de pe ecran.
Luați în considerare utilizarea modului grafic prin construcția graficului Y (x) = x c / (2 (x + 1) (x + 1)), în intervalul x Î [-5, -1) U (-1, 5] incrementează h, iar construirea asimptota dat de expresia Y (x) = x / 2 - 1.
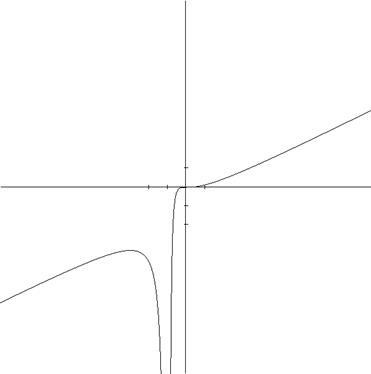
Funcții intabulare pot fi realizate cu următorii operatori:
pentru i. = 1 la n do începe
Aici vom introduce numele variabilelor: xStart - valoarea inițială a argumentului, xEnd - valoarea finală a argumentului, n - numărul de puncte într-un rând. Pasul modifică argumentul X este dată de:
h: = (xEnd -xStart) / (n - 1);
Valorile calculat organizat ciclu Funcția tabelare Y (x), folosind rutina - o funcție numită index F. fiecărei valori X și valoarea corespunzătoare a Y (x), vor fi plasate în anumite elemente ale matrice W. La punctul X = -1 nu este un dat funcție determinată, prin urmare, este necesar să se excludă din reprezentarea grafică a porțiunii în vecinătatea acestui punct. Acest lucru se realizează prin utilizarea operatorilor de software
dacă y [i] <- 6 then y[ i ] := - 6;
În acest caz, a efectuat o limită inferioară la nivelul y = -6, și toate valorile care sunt mai mici decât -6, vor fi excluse din reprezentarea grafică. Ca în cazul în care într-un cartier al funcției de decalaj ar primi o valoare pozitivă, ar fi să efectueze operații de introducere a operatorilor limită superioară
în cazul în care un - nivel limită.
Pentru a determina amploarea parcelelor grafic necesitatea de a găsi valorile minime și maxime ale elementelor de matrice Y. Acest lucru este realizat de către operatori
pentru i: = 1 la n do începe
dacă y [i]> Ymax apoi
dacă y [i] Pentru a instala modul de grafică, trebuie să utilizați procedura standard modulul InitGraph grafic care instalează unul din modurile posibile grafice. Proceduri următorul format: InitGraph (DriverName, modul put_k_drayveru); Modulul Graph oferă peste 70 de rutine. Luați în considerare procedurile necesare pentru construirea graficului Y = f (x) într-un interval predeterminat de variație X cu un pas predeterminat h. utilizați următoarele proceduri pentru formarea de antet program moleno: SetTextStule (Font, Direct, CharSize); Text de afișare -Procedura care indică tipul de font, și înclinarea dimensiunii sale. Tipul de font (parametrul Font) în modulul grafic definește constante: DefaultPont = 0 (tip matrice); TriplexPont = 1 (bold); SmallFont = 2 (tip mic); SansSerifPont = 3 (tip drepte); GothicPont = 4 (Gothic font). Pentru a determina direcția constantele de text folosite: Horizdir = 0 (stânga) sau VertDir = 1 (în sus). Al treilea parametru specifică dimensiunea fontului. Dacă CharSize = 1, simbolurile au dimensiunea convențională (8x8 pixeli) când CharSize == 2, simbolurile au aceleași dimensiuni 16x16 pixeli. Valoarea maximă a constantei este de 10. Procedura SetTextJustify (kod_gorizontali, kod_vertikali) - stabilește parametrii pentru distribuirea textului, în funcție de codul. Procedura OutTextXY (X, Y, text); - oferă o putere de text din coordonatele (X, Y). Atunci când se formează axa X, grilă orizontală și verticală se poate utiliza următoarea procedură: SetLineStile (tip_liniar, opredelenie_polzovatelem / vid_linii); - este determinată de tipul de linie: solidin = 0 (linie solidă), dottein = 1 (linie punctată), centerin = 2 (linia dot-dash), dashedin = 3 (linia punctată), bitin-user = 4 (o linie definită de utilizator); al doilea parametru este semnificativă numai atunci când userbitln = 4, iar vederea este definită printr-o linie constantă nonnwidth = 1 (grosime normala) sau thickwidth constantă = 3 (linie solidă); Setcolor (culoare) - determină culoarea de caractere și linii. Pentru a seta cursorul la numita procedură utilizată MoveTo, (X, Y) coordonează și pentru trasarea unei linii din linia curentă la coordonatele specificate - procedura LineTo (X, Y). Atunci când se lucrează cu imagini pe care doriți să utilizați sistemul de coordonate. În funcție de rezoluția ecranului selectat modul stabilit de imagine la 320x200, 640x480, sau alt număr de puncte (pixeli). Software-ul poate fi setat de numărul maxim de pixeli pe linie prin intermediul funcției GetMaxX, iar numărul de linii missing- prin intermediul funcției GetMaxY. Originea este setat la (0, 0), centru de ecran - (GetMaxX div 2, GetMaxY div 2), și colțul din dreapta jos - (GetMaxX, GetMaxY). Atunci când se efectuează operațiile grafice au indicat întotdeauna că ar trebui să facă cursorul, dar cursorul se invizibil în modul grafic.articole similare