Rezumat triunghi sferic și aplicarea acestuia 2

Triunghiul sferic și aplicarea acesteia.

triunghi sferic - o formă geometrică de pe suprafața sferei format de intersecția celor trei cercuri mari. Trei cercuri mari pe suprafața sferei care nu se intersectează la un moment dat, formează opt triunghiuri sferice. triunghi sferic, toate părțile din care mai puțin de jumătate dintr-un cerc mare, numit Euler.

Side sferică triunghi de repaus valoarea măsurată a unghiului central pentru ea. Unghiul triunghiului sferic Valoarea unghiului diedru între planurile în care se află parte a acestui unghi măsurat. Relațiile dintre elementele de triunghiuri sferice care studiază trigonometrie sferică.

Proprietățile triunghiului sferic:

1. În plus față de cele trei semne ale egalității de triunghiuri plane, triunghiuri sferice mai fidel una, două triunghiuri sferice sunt congruente dacă unghiurile lor corespunzătoare sunt egale.
2. Pentru părți sferice triunghi 3 sunt realizate inegalitatea triunghi: fiecare parte este mai mică decât suma celorlalte două părți și mai mult din diferența lor.
3. Suma tuturor laturile a + b + c este întotdeauna mai puțin 2PR.
4. Cantitatea 2πR - (a + b + c) se numește defect sferic
5. unghiuri sferice ale unui triunghi cu sumă s = # 945; + # 946; + # 947; întotdeauna mai mic decât 3π și mai mult π
6. Valoarea se numește un exces aplatizării sferic sau sferic
7. Aria triunghiului sferic definită prin formula.
8. Spre deosebire de triunghi plat în triunghi sferic pot fi două sau chiar trei unghiuri de 90 ° fiecare.

Dintre toate poligoanele sferice cel mai mare interes este triunghiul sferic. Trei cerc mare, se intersectează în perechi, la două puncte de pe forma sferă opt triunghiuri sferice. Cunoașterea elementelor (părțile și unghiuri) ale uneia dintre ele, se poate determina toate celelalte elemente, cu toate acestea, având în vedere relația dintre elementele unuia dintre ele, din care mai puțin de jumătate din toate laturile unui cerc mare. laturi ale triunghiului sunt măsurate prin unghiuri plane ale OABC colț triunghiulare, unghiuri ale triunghiului - unghiurile diedre colțului triunghiulare, vezi fig.

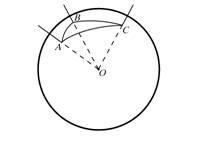
Proprietățile triunghiuri sferice diferă în mai multe moduri diferite, din proprietățile triunghiuri într-un plan. Astfel, cele cunoscute trei cazuri de egalitate triunghiuri rectilinii a adăugat un al patrulea: două triunghi ABC și A`V`S` egal dacă este egal, respectiv, trei unghi RA = RA`, PB = RV`, RS = RS`. Astfel, în domeniu, nu există triunghiuri similare, în plus, în geometria sferică nu este noțiunea de similitudine, întrucât nu există nici o schimbare, modificarea distanțelor în același (nu egal cu 1) numărul de ori. Aceste caracteristici se datorează încălcarea liniilor paralele axiome euclidiene si a geometriei hiperbolice inerente. Triunghiuri având elemente egale și orientări diferite, numite simetrice, astfel, de exemplu, triunghiuri și AS`S VSS`

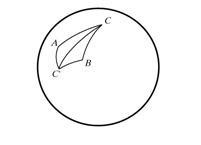
Dacă luăm în considerare un unghi lune o, apoi la 226 = 2p / n (n - un număr întreg) sferă poate fi tăiată uniform cu n copii ale Lune și zona sferei este egal 4pR2 = 4p când R = 1, zona deci lune este egal cu 4p / n = 2a. Această formulă este valabil și pentru a = 2PT / n și, prin urmare, este valabil pentru toate o. Dacă vom continua laturile unui triunghi sferic ABC, și să-și exprime domeniul de aplicare al zonei prin zona formată cu Lunes cu unghiuri A, B, C, și propria sa zonă, este posibil să se ajungă la formula de mai sus Girard.

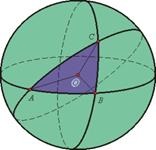
Într-un triunghi sferic poate fi două unghiuri drepte

Deja au un Varāhamihira indian (V-VI cenți.), Arabi matematicieni și astronomi de la IX. (Sabit Ibn Korra, al-Battani) și matematicienilor de Vest de Regiomontanus (XV c.), Găsit în diferite formulări teoremă remarcabil pe triunghiuri sferice. Iată cum poate fi formulată în notație modernă:

cosa = cosbcosc + sinbsinccosA. Sferice Teorema cosinus este foarte importantă pentru astronomie și geografie. Această teoremă ne permite să coordoneze cele două orașe A și B, pentru a găsi distanța dintre ele. În plus, matematicieni țările islamice sferice teorema cosinus ajută la rezolvarea o altă problemă practică: orașul cu coordonatele date pentru a găsi direcția de orașul sfânt Mecca (în fiecare musulman devotat ar trebui să se roage de cinci ori pe zi spre Mecca). Pentru a rezolva această problemă, în afară de orașul Mecca B, este necesar pentru a găsi unghiul A al triunghiului.

În astronomie, sferică teorema cosinus ne permite să treacă de la un sistem de coordonate pe sfera cerească la alta. Trei astfel de sisteme sunt cele mai frecvent utilizate: unul la ecuator este ecuatorul ceresc și poli - polii lumii, în jurul căreia există rotația zilnică aparentă a stelelor; celălalt este ecliptica ecuator - un cerc, în care pe tot parcursul anului se face mișcare aparentă a soarelui împotriva stelelor; un al treilea rol al ecuator îndeplinește orizont, și rolul poli - zenit și nadir. În special, datorită regulii cosinus sferice se poate calcula înălțimea soarelui deasupra orizontului la momente diferite și pe diferite zile ale anului.

Sails în arhitectură - triunghi sferic, oferind o tranziție de la un pătrat în planul spațiului cupola domului la circumferința. Sail, pandativ (de la părintele pendentif.) - o parte din bolta elementului dom prin trecerea de la baza dreptunghiulară la tavan cupolă sau tamburul acestuia. Sail are forma unui triunghi sferic, apexul înclinat în jos și umple spațiul dintre arcade podpruzhnymi care leagă stâlpii pătratului adiacente dom. Baze vele triunghiuri sferice în mărime, pentru a forma un cerc, și să distribuie sarcina arcelor cupola circumferință.

Dome pe vele

DzhordzhNelson (George Nelson)

„Proiectantul se pot relaxa oarecum și să se distreze ,. Rezultatul poate fi o glumă, distractiv este uimitor cât de des acest lucru se întâmplă foarte mult distractiv,“ Dzhordzh Nelson

Dzhordzh Nelson - proiectant american, arhitect, critic de design și teoretician. (1908, Hartford, Connecticut - 1986, New York)

corpuri proiectate de lumina, ceasuri, mobilier, ambalaje, angajate în expoziție de design.

Cele mai cunoscute proiecte de design George Nelson reprezinta stilizare magistral de forme geometrice, în spiritul op artă și abstracție geometrică.

Forma său celebru designer de scaun negru se bazează pe un triunghi sferic, este utilizat pe scară largă în planurile arhitecturale ale structurilor de tip dom. În special, în bisericile bizantine și românești, cum ar triunghi sferic numit „naviga“. Datorită „naviga“ o tranziție lină de la cupola suportului cupola.

Utilizarea unui triunghi sferic:

1. Utilizarea de grafică tridimensională triunghiuri sferice
2. În astronomie
3. În geografie. triunghi sferic Teorema permite coordonatele celor două orașe A și B, pentru a găsi distanța dintre ele.
4. În arhitektrue
5. În proiectarea unui scaun de George Nelson
6. gravarea

articole similare

• Triunghiul sferic și aplicarea acesteia