Rădăcini de unitate

Din aceste formule rezultă că rădăcinile unității sunt întotdeauna exact n. și toate sunt diferite.

Fiecare modul rădăcină este 1. În planul complex rădăcinile unității formează vârfurile unui poligon regulat. înscris în cercul unitate. Una dintre vârfurile este întotdeauna integrat unitate 1 + i 0.
Dacă u k> - o rădăcină de unitate, apoi conjugatul să-l numărul de u k ¯ >>> - este, de asemenea, o rădăcină de unitate.
Fie M - un punct arbitrar pe cercul unitate, și n> 1. Apoi, suma pătratelor distanțelor de la M la toate rădăcinile n-lea de unitate este egală cu 2 n.

Rădăcinile unității sunt numere întregi algebrice.
Rădăcinile unității formate prin multiplicarea grup finit comutativ de ordinul n. În special, orice rădăcină de putere integrantă a unității este, de asemenea, o rădăcină de unitate. Revers elementul pentru fiecare element al grupului coincide cu conjugat. Element neutru al grupului este unitatea complexă.
rădăcini grup de unități izomorfe la grupul aditiv al claselor de reziduuri Z n _>. Rezultă că este ciclică; ca sămânță (primitiv) poate lua orice u k> elementul. indicele k este relativ prim la n.
- consecinţe:
  - elementul u 1> este întotdeauna un primitiv;
  - în cazul în care n - prim. măsură orice rădăcină de ± 1. Acesta acoperă întregul grup;
  - numărul de rădăcini primitive este egal cu φ (n). în cazul în care φ - funcția Euler.
Dacă n> 1. atunci suma gradelor de orice rădăcină primitivă de unitate u au formula:

Σ k = 0 n - 1 u k = u n - 1 u - 1 = 0. ^ u ^ = - 1 = 0. >>>

rădăcini cub de unitate

Cube rădăcini de unitate:

Rădăcinile de gradul 4 al unității:

Pentru rădăcina al 5-lea grad sunt generatoare de element de 4:

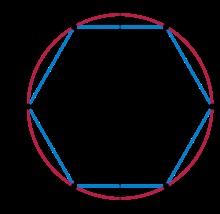
Roots 6 al unității ca primul grad al elementului de generare