Un set convex - subset al spațiului Euclidian care conține segmentul care unește două puncte de oricare din multitudinea.
Cu alte cuvinte, setul se numește convexă dacă:
Aceasta este, în cazul în care X împreună cu oricare două puncte care aparțin acestui set conține un segment de legătură pentru a le:
.
În spațiul seturilor convexe sunt drepte, jumătate de lungime a intervalului, un set-un singur punct.
Spațiul convexă este spațiul în sine, orice subspațiu, minge, tăiate, cu un singur punct de setul său liniar. De asemenea, sunt proeminente astfel de seturi:
- drepte. care trece prin punctul 0 în vector x direcția h:
;
- fascicul. care provine de la punctul x 0 în direcția vectorului h:
;
- hiperplan H p? cu p normal:
;
- jumătate de hiperplan care împarte spațiul:
,
.
Toate aceste seturi (în plus față de glonțul) este un caz special al unei multitudini de poliedre convexe.
Proprietățile seturilor convexe
- Intersecția seturi convexe este convexă.
- O combinație liniară a unei multitudini de puncte de convexe convexe.
- Un set convexă conține orice combinație convexă de punctele sale.
- Oriunde în spațiul Euclidian n-dimensional cu coca convexe a setului poate fi reprezentat ca o combinație convexă de cel mult n +1 puncte ale acestui set
Luați în considerare n - dimensional spațiu euclidian și lăsați- # 61485; punct în acest spațiu.
Luați în considerare două puncte și. aparținând puncte .Mnozhestvo. care poate fi reprezentat ca
(In coordonate este scris după cum urmează:
,
Se numește convexă și kombinatsieytochek
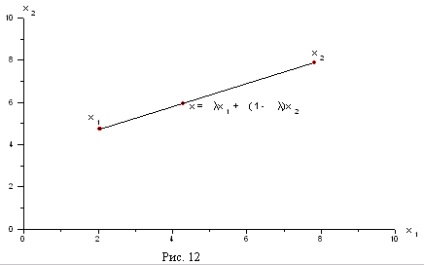
segment. care unește punctele și. ele însele puncte și sunt numite capetele segmentului. În cazurile de n = 2 și n = 3 este # 61485; segment în sensul obișnuit al cuvântului în planul sau în spațiu (vezi. fig. 12). Rețineți că, atunci când # 61548; = 0. și când # 61548; = 1. și anume la # 61548; = 0 și # 61548; = 1 obținem segmentul se termină.
,
în cazul în care totul se numește o combinație convexă de puncte.
Să fie o anumită regiune în spațiu (cu alte cuvinte,
G este un set de puncte
Definiția. Setul (zonă) este convexă. în cazul în care faptul că rezultă că # 61548; # 61646; [0,1]. Cu alte cuvinte, G # 61485; convexe set, în cazul în care este, împreună cu oricare două dintre punctele sale, conține un segment de legătură pentru aceste puncte.
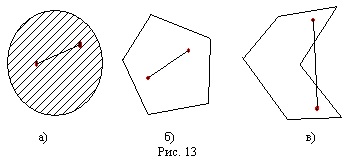
În aceste cifre, „a“ și „b“ - seturi convexe, și „c“ nu este un set convexă, pentru că există o astfel de pereche de puncte care segment de legătură pentru ele nu este toate fac parte din acest set.
Teorema 1. Fie G # 61485; convexe set. Apoi, orice combinație convexă a punctelor care aparțin acestui set, aparține, de asemenea, acest set.
# 61485; punct aparținând setului G.
Dovedim teorema prin inducție. Atunci când k = 2, teorema este adevărată, pentru că pur și simplu se mută în definirea unui set convexe.
Să presupunem că teorema este adevărată pentru unele k. Ia punctul și ia în considerare combinația convexă
,