Descrierea postului:
Tipul postului: munca de referință
Valoarea instantanee a tensiunii, determinarea curent amperaj pe baza datelor sale de valoare amplitudine. circuitul general, valoarea de amplitudine a tensiunii. Natura rețelei de încărcare de sucursale. Raportul dintre circuitul de putere utilă, site-urile reactive de tensiune.
Opțiuni de descărcare de detectare tensiune de circuit
Setări de încărcare, circuitul de detectare de tensiune
Definim curentul de acțiune, cunoscând valoarea sa de vârf
Găsiți rezistența totală a circuitului, ca rădăcina pătrată a sumei componentelor active și reactive de pătrate (așa cum este indicat de rezistența triunghiului):
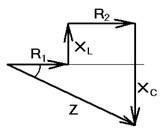
Să ne găsim circuitul de tensiune de funcționare generală (citire voltmetru 1), produsul din amperajul actuale privind rezistența totală a circuitului:
Vom găsi valoarea de vârf a tensiunii totale a circuitului:
Vom găsi unghiul de schimbare de fază de tensiune în raport cu curent
Scriem U1 (t) Tensiune valoarea instantanee:
u1 (t) = Umax * sin (# 61559; t + # 61537 + # 61546;) = 36,50 * sin (# 61559; t - 45 - 41) = 36.50 * sin (# 61559; t - 86);
Deoarece puterea porțiune de circuit activ (putere care prezintă un wattmetru) este definit ca produsul dintre patratul amperajul curent la rezistența acestei porțiuni, atunci:
Indicații două voltmetru. Pentru a găsi această valoare impedanță generată de rezistență R2 și capacitate CS:
Zadacha2. AC tensiune de rețea u incluse trei receptor paralel de energie, putere activă și factorul de putere, sunt cunoscute (a se vedea tabelul pentru acest lucru). Determina receptoare curenți și curentul într-o parte dreaptă a lanțului, și factorul de putere al instalației.
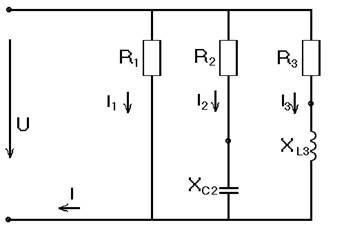
Am găsit rezistența totală a ramurilor 2 și 3, ca rădăcina pătrată a sumei pătratelor rezistenței și reactanței (semnul „-“ corespunde naturii capacitivă a sarcinii):
Găsim ramuri curente complete 1 și 2, ca porțiunea de raport de tensiune 2-3 la rezistența totală a fiecărei ramuri:
Noi găsim raportul dintre ramurile puterii utile 1 și 2, ca raportul dintre ramurile de rezistență la impedanța de ramură:
Găsim componentele active ale ramurilor curente 1 și 2, produsul din totalul ramurilor actuale ale raportului dintre ramurile puterii utile:
Găsim componente reactive curente ramuri 1 și 2, rădăcina pătrată a diferenței pătrat completă și curenții activi (semnul „-“ corespunde curentului capacitiv, adică XC> XL):
Am găsit porțiunea componentă activă și reactivă 2-3 ca suma componentelor active ale ramurilor 2, 3 și reactive componente ale ramurilor 2, 3, respectiv (în care semnul „-“ corespunde cu curentul capacitiv):
Am găsit curent bucla completă, ca rădăcina pătrată a sumei pătratelor porțiunii curenților activă și reactivă 2-3:
Descoperim porție tensiune 1-4 (activ), ca produs al curentului total din circuitul de rezistență R1:
Găsim porțiune de 4-5 tensiune (inductiv) ca produs total circuitul de curent la XL1 reactanță inductivă:
Am găsit porțiunea 5-2 tensiune (capacitiv) ca produs al curentului total din circuitul XS1 capacitate:
Am găsit o porțiune de tensiune activă 2-3, ca produs al porțiunii de tensiune 2-3 cu un factor de putere utilă porțiune de 2-3 (având în vedere faptul că coeficientul de porțiunii de putere utilă 2-3 este raportul dintre activ la un total de curent):
Am găsit porțiunea de tensiune reactanță 2-3, ca rădăcina pătrată a diferenței pătrat plin și tensiunile active (unde semnul „-“ corespunde tensiunilor capacitiv, adică Ir23 0,5 * E1 + 2 0.5 * j * E1 = I1 * R1 - I3 * j * 1 / WC3 + I3 * R3;
Pe baza celei de a doua lege a lui Kirchhoff pentru circuitul bcab:
Un sistem de 3 ecuații:
Se determină complexele curenți care operează în toate ramurile, cele două noduri folosind metoda.
E1 = 240 * e J45 = 170 + 170j (B);
XC2 = - 1 / w C2 * e J90 = - 1 / (2 * 3.14 * 500 * 100) = - 3,18 * e J90 (ohmi);
Xc3 = - 1 / w C2 * e J90 = - 1 / (2 * 3.14 * 500 * 50) = - 6,37 * e J90 (ohmi);
Scriem în jos ramurile de rezistență în formă complexă:
Găsim conductivitatea de ramuri:
Am găsit tensiunea între nodurile a și b:
Uab = (240 * e * J45 1/12 * e j0 - 240 * e * j0 1 / 21,94 * e J90) / (1/12 j * 1 / 21,94 + + + 0.11405 0.12460 * j) = (20 * e J45 -10.97 * e J90) / (0.19738 + 0.07902 * j) = (14.14213-3.17213 * j) / (0.21261 * e j21.8) = 68,17 * e - j9;
Noi găsim curenții de circuit:
Conform rezultatelor obținute la punctul 2, definește wattmetrului în două moduri:
a) prin utilizarea expresiile pentru complexe de curent și tensiune;
b) în conformitate cu formula UIcos (UI):
P = UIcos (UI) = 197.76 * 16.48cos (59 - 45) = 3162.3 (W);
Vom construi o diagramă topografic, combinate cu diagrama vector de curent.
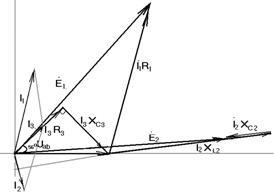
Construiți o diagramă radială pentru curentul în a doua ramură atunci când modulul de schimbare de rezistență acea ramură de la 0 la # 61605;. Pentru a găsi acest curent Ik maxim rezistând al treilea aspect este egal cu 0:
Am găsit o rezistență de circuit în raport cu o clemă și b:
coardă este Ik = 14,53 * e 12.8;
factor este k = 0,36;
unghiul înscris # 61561 = - 7
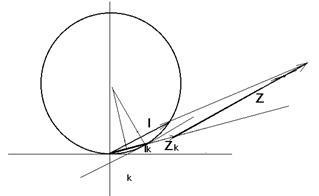
Folosind un model circular construi un grafic al schimbării acestui curent depinde de rezistența modulului.
Folosind datele de calcul primite în pasul 2, putem scrie expresie pentru instantanee valorile de curent și tensiune. Noi construim un grafic al uneia dintre aceste cantități.
I2 = 11,51 * sin (wt + 36,53)
Program - SINEWAVE, mutat ou relativă 9 și 0-36.53 0, respectiv.
Presupunând că cele două inductanțe aranjate în diferite ramuri ale unui sistem dat, există un cuplaj magnetic cu un coeficient de flux magnetic M (se adaugă un al doilea inductanță 3 ramură) compun o formă generală a sistemului de ecuații pentru a calcula curenții în toate ramurile lanțului, scriindu-l în două forme:
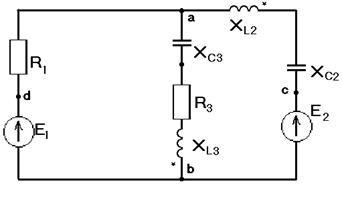
1) Pe baza legilor Kirchhoff formează, în general, sistemul de ecuații pentru a calcula curenții în toate ramurile lanțului, scriindu-l în două forme:
a) diferențial. Pe baza legii prima Kirchhoff pentru site-ul și:
Pe baza celei de a doua lege a lui Kirchhoff pentru circuitul bdab:
Pe baza celei de a doua lege a lui Kirchhoff pentru circuitul bcab:
Un sistem de 3 ecuații:
Pe baza legii prima Kirchhoff pentru site-ul și:
Pe baza celei de a doua lege a lui Kirchhoff pentru circuitul bdab:
Pe baza celei de a doua lege a lui Kirchhoff pentru circuitul bcab:
Un sistem de 3 ecuații:
Problema 5. Motor Two AC conectat în paralel cu circuitul cu o tensiune u2 și de lucru cu cos # 61546 factor de putere mică; 1. dispozitive în fiecare dintre curenții de circuit cu motor show-I1 și I1 și P1 și P2 puterea de măsurare. fire de linii electrice sunt R0 rezistență și x0 inductiv. Valorile numerice ale tuturor variabilelor necesare pentru calculul sunt enumerate în tabelul de opțiuni. trebuie:
A. Se calculează predeterminate circuit electric și pentru a determina (pentru a conecta condensatori):
Tensiunea de la începutul liniei
Pierdere și cădere de tensiune pe linie
Energia electrică activă, reactivă și aparentă la capătul liniei și pierderea puterii în firele
factor de capacitate de plante
Unitatea de compensare B. Se calculează pentru a produce cos # 61546; 2 = 0,95 și pentru a determina valorile pentru respectivul factor de putere și capacitatea de putere de condensatoare.
B. Executarea circuitului de calcul prevăzut setare operațiune de compensare, și pentru a găsi valoarea specificată la punctul A. Rezultatele sunt tabelate și comparate pentru diferite moduri de funcționare a motorului (înainte de compensare și cos # 61546; 2 = 0,95). Mark, ce concluzii oferă unitate de corecție a factorului de putere.
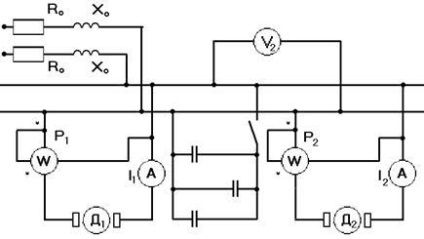
A. Gasim rezistență fiecărui motor bazat pe faptul că puterea activă este produsul rezistenței la ramuri pătratice curente. Deci:
Noi găsim puterea reactivă a fiecărui motor ca produs al curentului de tensiune:
Găsim capacitatea maximă a fiecărui motor, ca rădăcina pătrată a diferenței dintre puterea aparentă și activă:
Am găsit reactanța fiecare motor electric bazat pe faptul că puterea reactivă este produsul reactanță la sucursala pătrat curent (reactanță este inductiv):
Am găsit rezistența totală a fiecărui motor, bazat pe faptul că rezistența totală este egală cu rădăcina pătrată a sumei pătratelor componentelor reale și reactive:
Găsim conductanța porțiunii paralele:
Găsim porțiune paralelă susceptance:
Găsim conductivitate porțiune paralelă, în ipoteza în care admiterea este egală cu rădăcina pătrată a sumei pătratelor componentelor sale reale și reactive:
Gasim plin curent bucla ca produs de tensiune la porțiunea paralelă porțiune paralelă conductivitatea:
Forma porțiunea de circuit echivalent pentru înlocuirea rezistența echivalentă paralel și reactanța:
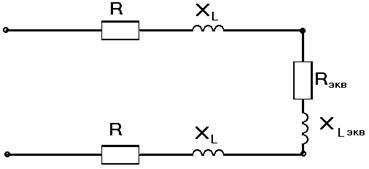
Noi găsim rezistențele și reactanțele porțiunii paralele echivalente:
Am găsit impedanța porțiunii paralele:
Am găsit rezistența activă totală a circuitului (suma tuturor rezistențelor):
Am găsit rezistența totală a circuitului reactanței (suma tuturor Reactanta):
Am găsit rezistența totală a circuitului, ca rădăcina pătrată a sumei pătratelor rezistenței și reactanței:
Z = (XL 2 + R2) 0,5 = 1.531 (Ohmi);
Am găsit tensiunea circuitului totală a circuitului activitatea curentă totală pe impedanța circuitului:
Cunoașterea plin curent al circuitului, găsiți căderea de tensiune în liniile de cabluri de pe rezistența activă:
Cunoașterea plin curent al circuitului, găsiți căderea de tensiune în firele de pe linia reactanța:
Am găsit căderea totală de tensiune a circuitului în linia de cabluri ca rădăcina pătrată a sumei pătratelor căderea de tensiune în firele de pe rezistența liniei și reactanță:
Am găsit puterea activă, reactivă și aparentă la capătul liniei și pierderea puterii în firele, presupunând că puterea totală la sfârșitul liniei este egală cu produsul tensiunii totale liniei curente la sfârșitul liniei:
P = I 2 * R12 = 27,008 (W); Q = I 2 * XL12 = 22579 (W);
S = (P + 2 + Q 2) 0,5 = 35202 (W);
Vom găsi factorul de putere al instalației:
Am găsit raportul liniei de transmisie a puterii utile:
B. Se calculează unitatea de compensare pentru a produce cos # 61546; 2 = 0,95 și definesc valorile pentru respectivul factor de putere și capacitatea de putere de condensatoare.
Vom înlocui această diagramă a unui echivalent pe baza rezultatelor obținute în PA
Lăsați capacitatea de condensatoare este ohmi XC. Găsim paralel porțiune de conductivitate.
Găsim porțiune paralelă susceptance:
Găsim conductivitate porțiune paralelă, în ipoteza în care admiterea este egală cu rădăcina pătrată a sumei pătratelor componentelor sale reale și reactive:
Vom înlocui această diagramă a unui echivalent, înlocuind porțiunea cu legarea în paralel a rezistentei la Zpar activ-inductive:
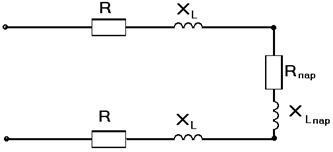
Rpar = g / y = 0558 2 / (0.311364 + (0467 - 1 / XC 2) 2);
Am găsit rezistența activă totală a circuitului (suma tuturor rezistențelor):
Am găsit rezistența totală a circuitului reactanței (suma tuturor Reactanta):
Să ne rezolve ecuația cu respect XC 2
1 = 0.654 * (0,311364+ (0.467-1 / XC 2) 2) + 1,8 * (0.467-1 / XC 2)
(0.467-1 / XC 2) = 1,376 + 1,850 = 3,226
Deci, capacitatea de condensatoare este:
V. Să completeze rezistența activă a circuitului (suma tuturor rezistențelor):
Am găsit rezistența totală a circuitului reactanței (suma tuturor Reactanta):
Am găsit rezistența totală a circuitului, ca rădăcina pătrată a sumei pătratelor rezistenței și reactanței:
Z = (XL 2 + R2) 0,5 = 1,09 (Ohm);
Am găsit bucla de curent ca tensiunea de circuit complet la impedanța circuitului:
Cunoașterea plin curent al circuitului, găsiți căderea de tensiune în liniile de cabluri de pe rezistența activă:
Cunoașterea plin curent al circuitului, găsiți căderea de tensiune în firele de pe linia reactanța:
Am găsit căderea totală de tensiune a circuitului în linia de cabluri ca rădăcina pătrată a sumei pătratelor căderea de tensiune în firele de pe rezistența liniei și reactanță:
Am găsit puterea activă, reactivă și aparentă la capătul liniei și pierderea puterii în firele, presupunând că puterea totală la sfârșitul liniei este egală cu produsul tensiunii totale liniei curente la sfârșitul liniei:
P = I 2 * R12 = 50459 (W);
Q = I 2 * XL12 = 11213 (W);
S = (P + 2 + Q 2) 0,5 = 51,690 (W);
Vom găsi factorul de putere al instalației:
Am găsit raportul liniei de transmisie a puterii utile:
Întocmește un tabel de sinteză: