Împreună cu o abordare spectrală la descrierea semnalului în practică, de multe ori devine caracteristicile necesare, ceea ce ar da o idee despre proprietățile de semnal, în special, rata de schimbare în timp. precum și durata semnalului fără a se descompune in componentele sale armonice.
Ca o astfel de caracteristică temporală este larg utilizată funcția de corelare a semnalului.
Pentru S (t) al funcției de corelare a semnalului deterministic durată finită este determinată de următoarele expresii:
în care - semnalul de decalare.
Aici vom lua în considerare semnalele, care sunt reale funcții de timp, și, prin urmare, desemnarea conjugare complexă poate fi omise.>
De la (0.129), care caracterizează gradul de conectare (corelare) a semnalului S (t) cu copia sa deplasat cu o valoare de-a lungul axei de timp. Este clar că funcția atinge un maxim atunci când, pentru că orice semnal este complet necorelate cu ea însăși. În acest caz,
Adică valoarea maximă a auto - funcția de corelare este egal cu energia semnalului.
Odată cu creșterea scade (nu neapărat monotonă) și cu o deplasare relativă a semnalului S (t) și un timp care depășește durata semnalului dispare.
Figura 2.36 arată construcția funcției de corelare pentru un simplu semnal într-un puls rectangular (Fig. 2.36.a). Decalate cu Fig. 2.36-b, iar produsul - în Fig. 2.36-in. Diagrama funcției prezentată în Fig. 2.36,2. Fiecare valoare corespunde produsului și aria sa sub graficul functiei. Valorile numerice ale acestor zone pentru funcțiile respective și da ordonata.
O construcție similară pentru impulsul triunghiular este prezentat în Fig. 2.37. Din definiția generală a funcției de corelare, și după cum se poate observa din aceste exemple, care imateriale spre dreapta sau spre stânga în raport copia sa mutat de cantitatea de semnal. Prin urmare, expresia (2.129), pot fi rezumate după cum urmează:
Acest lucru este echivalent cu a spune că este o chiar funcționează Naris. 2,38, și arată semnalul sub formă de pachete de 4 impulsuri identice care sunt deplasate unul față de altul, în timp, și Fig. 2.38-b - corespunzător acestui semnal, funcția de corelare. Valori apropiat. egal cu 0, iar această funcție are aceeași formă ca și pentru un singur impuls (vezi. Fig. 2.36-2).
Valoarea maximă a funcției de corelare (at) este egală cu de patru ori energia un impuls.
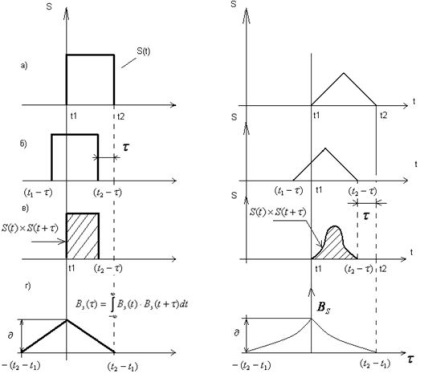
Fig. Figura 2.36. 2.37 Build korrelyatsi-
Construcția funcțiilor de corelare pentru triunghiulară a acestora
Funcția de puls dreptunghiular.
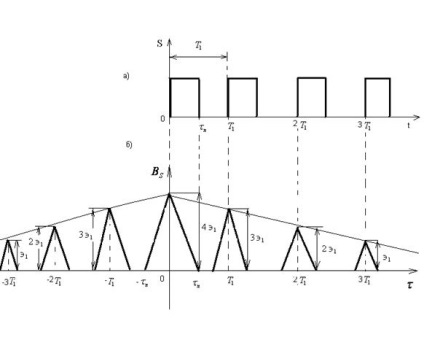
Fig. 2.38. Pachet de 4 impulsuri pătrat (a) și funcția de corelare a exploziei (b).
Pentru un semnal periodic a cărui energie este infinit de mare, determinarea funcției de corelare folosind expresia (2.129) și (2.129 „) nu este acceptabil. În acest caz, pe baza următoarelor definiții:
Cu această definiție a funcției de corelare devine dimensiunea puterii. Este egală cu puterea medie a semnalului periodic.
Din cauza periodicitatea semnalului S (t) prin medierea muncii depuse sau T infinit de mare interval ar trebui să coincidă cu perioada dintre media. Prin urmare, expresia (2.131) poate fi înlocuită cu expresia:
Inclus în această expresie integralele nu este nimic altceva cum ar fi intervalul de semnal korrelyatsionnayafunktsiya. Notând-l prin, am ajuns la relația:
Evident, semnalul periodic S (t) corespunde funcției de corelare periodică. Perioada Funcția coincide cu o perioadă de S (t) a semnalului original.
De exemplu, cele mai simple (armonice) oscilațiilor
Atunci când, -Există amplitudinea medie a puterii de oscilații armonice.
Important, funcția de corelare este independentă de faza inițială de oscilație.
În (fig. 2.39-b) prezintă un semnal reprezentativ funcție de corelare a unei secvențe periodice de impulsuri dreptunghiulare (Fig. 2.39-a).
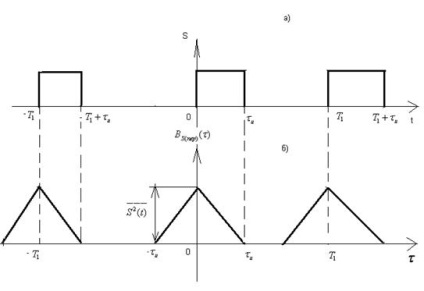
Fig. 2.39. secvență periodică de impulsuri (a), precum și funcția de corelare (b).
Fiecare dintre funcția impulsului coincide în forma cu funcția de corelare a unui singur impuls al secvenței periodice S (t). Cu toate acestea, în acest caz, energia maximă nu este egal coordona (ca în Fig. 2.38), iar puterea S semnal mediu (t), adică magnitudine.
Pentru a evalua gradul de corelare între două semnale diferite și funcția de corelare încrucișată este determinată de expresia generală:
Pentru funcțiile reale
Funcția de corelare de mai sus este un caz special al unei funcții atunci când.
Construcție funcției de corelare încrucișată pentru cele două semnale, și este prezentat în ris.2-40. Poziția de pornire este prezentată a semnalului (Fig. 2.40-a). Când semnalul de deplasare la stânga (Fig. 2.40, b) funcția de corelare de la primele creșteri și apoi scade la zero la.
Atunci când deplasarea spre dreapta (), funcția de corelare scade imediat. Rezultatul este asimetric în raport cu funcția ordonata (Fig. 2.40-in).
Este evident că valoarea nu se modifică în cazul în care în loc să feedforward semnal de la un semnal de întârziere.
Prin urmare, (2,134) pot fi rezumate după cum urmează:
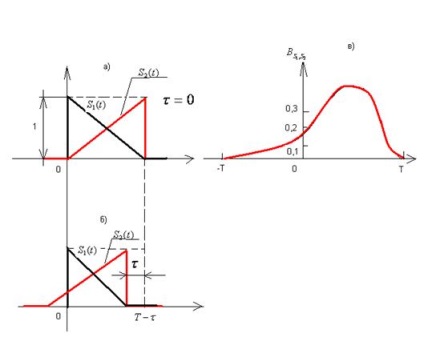
Fig. 2.40 Construirea unei funcții de corelare încrucișată:
a) începând semnale de poziție;
b) trecerea la semnalul din stânga;
c) funcția de corelare încrucișată.
Ar trebui, cu toate acestea, distincția între (2.129) și (2.135 „).
Spre deosebire de funcția de corelare otvzaimnaya nu este neapărat o chiar relativă. În plus, funcția de corelare încrucișată nu este în mod necesar atinge un maxim la. Ambele proprietăți ale funcției de corelare încrucișată ilustrată în ris.2.40.