Principiul mecanic al relativității. Transformarea Galileo.
În mecanica clasică, principiu mecanică corectă a relativității: legile dinamicii sunt aceleași în toate sistemele de referință inerțiale.
Luați în considerare două cadre: sistem inerțial K (coordonatele x, y, z), consideră în mod convențional pentru a fi fixat și un sistem de K „(cu x coordonatele“, y „z“), se deplasează în raport cu un mod uniform și liniar cu υ0 viteză ( υ0 = const)
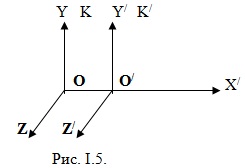
Coordonatele punctului A în raport cu rama K: x = x „+ 00“, pentru un interval de timp t de origine ar fi:
Ecuațiile (3.19) sunt numite transformarea de coordonate și timpul Galileo. Numărătoarea inversă a început din momentul în care originea celor două sisteme coincid. Diferențierea în raport cu timpul t, obținem expresia regulii plus vitezei în mecanica clasică: υ = υ „+ υ0 (3,20)
Accelerații în ambele cadre sunt identice, ceea ce înseamnă că comportamentul organismelor în ambele sisteme aceeași: a = a „(3,21), adică din relația (3.21) confirmarea principiului mecanic al relativității urmează: ecuația dinamicii la trecerea de la un sistem de referință inerțial la altul nu sunt modificate, adică, Ele sunt invariante în raport cu transformările galileeni. Principiul mecanic al relativitatii poate fi formulată după cum urmează: orice experimente mecanice, efectuate în cadrul inerțial de referință, este imposibil să se stabilească dacă este în repaus sau se deplasează uniform într-o linie dreaptă. De exemplu, stând în cabina unei nave se deplasează uniform într-o linie dreaptă, nu putem determina nava este în repaus sau în mișcare, nu uită pe fereastră.