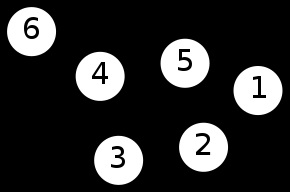
Acest grafic are r = contur rang 2. deoarece acesta poate fi transformat într-o îndepărtare copac a două margini, cum ar fi marginile 1-2 și 2-3, dar numai o singură muchie de ștergere părăsește bucla în grafic.
În teoria grafurilor, un rang buclă [1] al unui graf neorientat - acesta este numărul minim de muchii a căror îndepărtare distruge toate ciclurile contelui, transformându-l într-un copac sau o pădure. Rangul de contur poate fi înțeleasă ca un număr de cicluri independente din grafic. Dimpotrivă, problema corespunzătoare de a găsi un set de cicluri forward arce [ro] la grafice direcționate. buclă rang r poate fi ușor calculat cu formula
unde m - numărul de muchii ale unui anumit grafic, n - numărul de noduri. și c - numărul componentelor conectate [2]. Este de asemenea posibil să se construiască în mod eficient o multitudine de nervuri dimensiune minimă de descompunere cicluri folosind un algoritm greedy. sau adăugarea unui arbore de acoperire.
Locul de contur este, de asemenea, cunoscut sub numele de numărul cyclomatic al graficului. Ea poate fi explicată în termenii teoriei graficului algebrică ca dimensiunea spațiului ciclic [en] a graficului, în matroids termeni utilizând concepte corank graph matroids [en] [3] în ceea ce privește topologia și unul dintre Betty spațiu topologic numerele care derivă din grafic. Locul contur contorizează numărul de urechi în descompunerea urechii a graficului, care oferă baza pentru conceptul de complexitate parametrizate [ro] pe copaci și aproape utilizate în software-ul de valori, ca parte a determinării complexității cyclomatic a fragmentului de cod. Conceptul de complexitate cyclomatic Intitulata a fost introdus de Gustav Kirchhoff [4] [5].
Locul matroide înainte și construirea unui set minim de cicluri de [| ]
Conturul graficului G rang poate fi descrisă de teoria matroids cum graficul corank matroide [en] G [6]. Având în vedere proprietatea lăcomiei matroids, ceea ce înseamnă că este posibil să se găsească un set minim de muchii care distruge toate ciclurile, folosind algoritmul greedy. selectarea la fiecare nervură etapă aparținând cel puțin un ciclu al graficului rămase.
Pe de altă parte, un set minim de seturi, care distruge toate ciclurile pot fi găsite prin construirea unei păduri se întinde de G și selectați setul complementar de muchii care nu fac parte de pădure se întinde.
Numărul de cicluri independente [| ]
În teoria grafurilor algebrică. contur rang - dimensiunea spațiului ciclic [en] graficul G. Intuitiv, se poate explica rangul schiță ca numărarea numărului de cicluri independente ale graficului, în care setul de cicluri este considerat a fi independent dacă este imposibil să se formeze o buclă ca diferența simetrică a unui subset al celorlalte cicluri [2].
Acest calcul este de cicluri independente pot fi explicate printr-o teorie omologie. ramură topologiei. Orice graf G poate fi considerată ca un exemplu al unui complex simplicial 1-dimensional. un tip de spațiu topologic. formate de fiecare segment de reprezentare margine și legarea acestor segmente la capete. Este numărul cyclomatic de prim rang (întreg) al omologia complexului [7]
În legătură cu un astfel de număr topologică cuplare cyclomatic a graficului G este, de asemenea, numit un prim număr de Betty graf G [8]. Mai general, primul număr Betti al oricărui spațiu topologic contorizează numărul de cicluri independente în spațiu.
Aplicații [| ]
Coeficientul de reticulatia [| ]
Opțiunea contur rangul unui grafic plan. normalizate prin împărțirea la rangul maximă posibilă a oricărui grafic planar contur cu același set de noduri, numit coeficientul de reticulatie. Pentru graficele conectate cu margini plane m și n vârfuri Coeficientul reticulatie poate fi calculat prin formula [9]
În această formulă, numărătorul m # X2212; n + 1 în formula este un grafic contur al acestui rang și numitorul 2 n # X2212; 5 este cel mai înalt posibil rang plane Graficul de contur cu n noduri. Factorul reticularea se situează între 0 și 1 pentru arbori pentru graficele planare maxime [en].
Ureche de descompunere [| ]
Contur Locul reflectă numărul de urechi în descompunerea urechii a graficului, graficul descompunerea marginilor pe cale și ciclul care este adesea util în algoritmi grafic. În special, vârful graficului este 2-conectat dacă și numai dacă are o secvență deschisă descompunerea urechii a subgrafurilor în care primele sub-cutii este un simplu ciclu, iar restul de sub-coloane sunt moduri simple și începe fiecare mod și se termină la nodurile aparținând subgrafurilor anterioare, și fiecare nod intern al căii apare pentru prima dată în acest fel. In orice Graficele Connected cu profil rang r orice descompunere urechea deschisă a r exact urechi [10].
Aproape copaci [| ]
Grafic cu numărul cyclomatic r este numit, de asemenea, r aproape -tree. pentru că doriți să eliminați din grafic numai marginile r pentru a transforma într-un copac sau o pădure. Aproape 1-copac este aproape un copac - copac este conectat aproape psevdolesom. inel cu arbore (eventual banal) înrădăcinat la fiecare nod [11].
Generalizarea pentru graficele îndreptate [| ]
Locul Ciclic [en] - este grafice orientate invariante. măsurarea nivelului ciclurilor cuibărit în grafic. Această definiție este invariantă mai complexă decât Locul cyclomatic (în strânsă legătură cu definirea adâncimea arborelui pentru graficele neorientate) și calculul este mult mai complicat. O altă problemă pentru graficele direcționate legate de rangul cyclomatic - definirea unui set minim de arce transmite bucle [en]. adică, un set minim de arce a căror îndepărtare distruge toate ciclurile îndreptate. Ambele probleme, ciclul de calcul al rangului și determinarea setului minim de arce rarezayuschiego cicluri sunt NP-greu.
De asemenea, este posibil să se calculeze un simplu invariant de grafice orientate, dacă ignorați direcțiile de margini și se calculează rangul unui grafic neorientat ciclic. Acest principiu constituie baza pentru determinarea complexității cyclomatic. masoara complexitatea unui program de calculator pentru a evalua complexitatea cod de computer fragment.
Concepte înrudite [| ]
Alte numere definite în ceea ce privește marginile de îndepărtare a graficului neorientat includ conectarea la coaste. numărul minim de muchii, al cărei îndepărtare duce la pierderea conectivității și numărul de corelări de prevenire [en]. numărul minim de muchii, din care îndepărtarea duce la pierderea existenței unei potrivire perfectă.