schimbare în curent sau tensiune în timp, pot fi reprezentate prin diferite linii sau diagrame. curent continuu este neschimbat în timp, o linie dreaptă este prezentată (Figura 3.1 (a).), și curent alternativ - cele mai diferite curbe. Forma curbei de curent reflectă modificarea periodică a valorii curentului de maxim la minim, iar apoi din nou la maxim, și așa mai departe. D. (Fig. 3.1 (b)). Mai multe dintre curbele prezentate în Fig. 3.2.
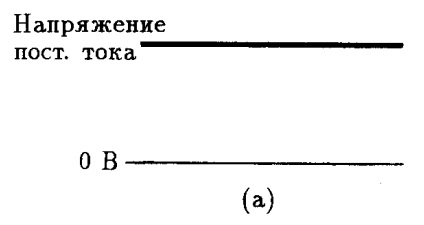
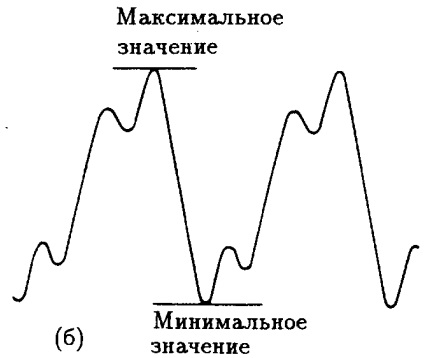
Fig. 3.1. Programeaza o constantă (a) și variabila (b) curentii
porțiune repetată a semnalului de curent alternativ numit un semnal de ciclu. Astfel, curbele prezentate în Fig. 3.2, punctul A este începutul ciclului, și punctul B - sfârșitul și începutul următorului ciclu.
Numărul de cicluri de semnal în unitatea de timp se numește frecvența semnalului. Unitate de măsură a frecvenței - hertz (Hz). De exemplu, în cazul în care semnalul se schimbă ciclul se repetă o dată pe secundă, frecvența semnalului este de 1 Hz dacă este de 10 ori - (. Figura 3.3) 10 Hz.
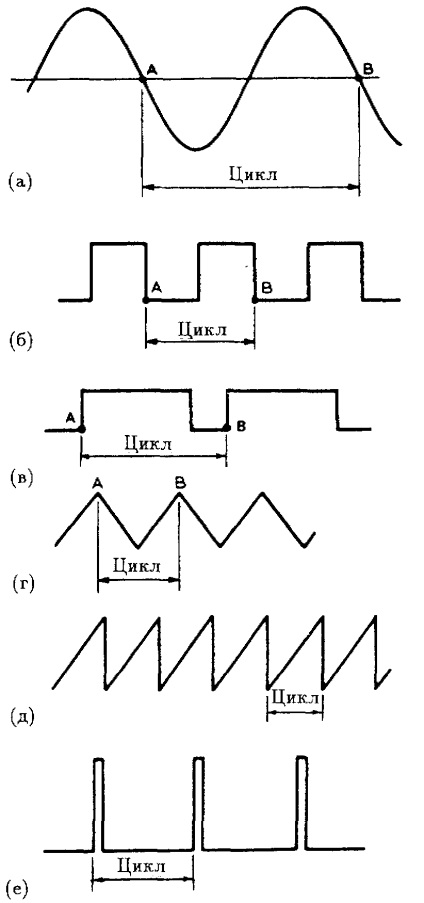
Fig. 3.2. Tipuri curbe AC: sine (a), pătrat (b), rectangulare (b), triunghiulare (g), sawtooth (d), impulsurile (e).
Timpul pentru care completează un semnal de schimbare completă ciclu, numit durata perioadei T, sau pur și simplu perioadă. De exemplu, în cazul în care semnalul trece toate modificările pe secundă, perioada sa este egal cu 1 când o jumătate de secundă, atunci perioada este de 0,5 secunde.
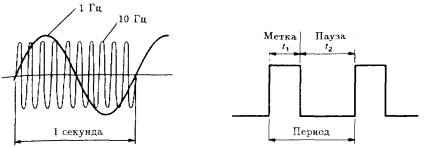
Fig. 3.3. Semnale de frecvențe diferite. Fig. 3.4. Factorul de umplere mai mic de 1.
Un perioadă val pătrat ar putea fi împărțită în marcaj (Mark) și pauză (spațiu) (fig. 3.4). Raportul dintre lungimea etichetei la lungimea pauzei se numește ciclul de lucru. În cazul în care etichetele durata t1 și t2 pauză, apoi
Durata t1 etichetei
Deoarece semnalul face un ciclu complet de schimbare pentru o perioadă,
Perioada = t1 + t2.
În cazul în care taxa este 1, atunci
Durata t1 etichetei = Pauză de timp t2.
Acest lucru poate fi scris în mod diferit:
Perioada = 2 * Pauză de timp = 2 * Lungime etichetă.
ƒ Unități de frecvență:
hertz, Hz; kilohertzi, kHz; megahertzi, MHz.
Perioada Unități de T:
ms, ms = 1/1000 = 10 -3 s
microsecundă 1/1000 ms = ms = 10 ms = 10 -3--6
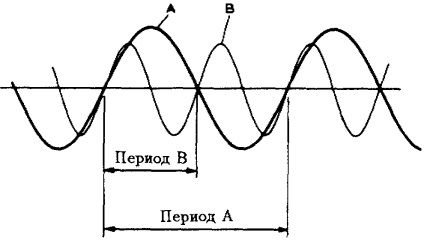
Raportul dintre frecvența și perioada
Luați în considerare graficele de semnal în Fig. 3.5. Semnalul are o frecvență mai mare decât semnalul A, dar perioada semnalului B este jumătate din perioada semnalului A. Cu o creștere scade sale de frecvență semnal perioadă, dimpotrivă.
Tabelul următor conține raportul unităților de măsură de frecvență, și perioada. Este util dacă vă amintiți.
Undele sonore sunt produse în aer, de exemplu, atunci când cineva spune sau difuzorul, sau un burghiu pneumatic, la reglarea diapazonul, și așa mai departe. Undele D. sonore modifică presiunea aerului și este necesar aerul pentru ei să se răspândească.
Intensitatea undelor sonore se caracterizează prin volum, ton caracterizează frecvența lor. Atunci când frecvența este schimbat de sunet ton.
Gama de frecvențe sonore, care sunt percepute de urechea umană, se numește gama de frecvențe audio. Se extinde de la 20 Hz până la 20 kHz. Sunetele de o frecvență mai mică de 20 Hz și peste 20 kHz persoană nu poate auzi. Pe baza acestui fapt, un fluier special pentru câine, făcând semn. Frecvența semnalului sonor al unui fluier mare de 20 kHz, astfel încât câinele având o gamă mai largă de frecvență de sensibilitate a urechii, ea, și oamenii aud - nr.
tonuri curate și instrumentale
ton pur numit oscilație sinusoidală simplă, cuprinzând o singură frecvență (Fig. 3.2 (a)). Instrumentul este un vobulată complex ton, constând dintr-o serie de unde sinusoidale de frecvențe diferite (Fig. 3.1 (b)). Aceste vibrații sonore apar atunci când sunetele de vorbire sau muzică.
Când adăugați mai multe frecvențe diferite undă sinusoidală apare oscilație complexă. Dimpotrivă, semnalul de complicat poate fi descompus într-un număr de oscilații sinusoidale sale constitutive pure. Printre acestea simplu oscilație sinusoidală distinse armonici armonice și de bază sau primul set. Astfel, orice semnal compozit poate fi descompus în următoarele componente:
1. Primul sau primar, armonică. undă sinusoidală simplă având aceeași perioadă ca și oscilație complexă inițială.
2. Un set de armonici. multipli simplu sinusoidală frecvenței de oscilație ko¬toryh ale frecvenței fundamentale. De exemplu, dacă frecvența primei armonici este de 100 Hz,
frecventa 2a armonic = 2 * 100 = 200 Hz;
frecvență treia armonică 3 * = 100 = 300 Hz;
frecventa 4a armonic = 100 * 4 = 400 Hz, și așa mai departe. d.
Cu cât numărul m armonic. E. Cu cât viteza, cea mai mică amplitudinea acesteia. Prin urmare, armonici mai mari sunt de obicei neglijate.
smoală
Înălțimea tonului de undă de sunet indică o parte din gama de frecvențe audio este frecvența.
sunete pătrunzător ocupă jumătatea superioară a intervalului de frecvență audio, și sunetele low-pitched - jumătatea inferioară. vocile femeilor au de obicei un pas mai mare decât bărbații. Drum emite sunete joase, un flaut - este foarte mare într-o frecvență de oscilație complexă a undei fundamentale determină tonalității semnalului.
calitatea sunetului
Calitatea sunetului este determinată de numărul de armonici de semnal instrumentale care sunt reproduse fără distorsiune a echipamentului.
Exemple ale unor semnale complexe
1. Basic + armonic treia armonică (Fig. 3.6).
2. Principalul armonic + 2a armonic (fig. 3.7).
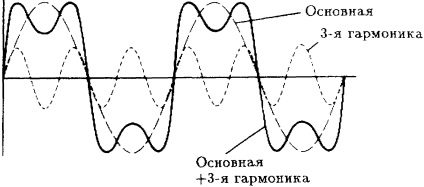
Fig. 3.6. Rezumat armonic + treia armonică (apropierea de undă dreptunghiulară).
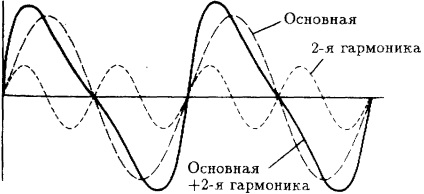
Fig. 3.7. Rezumat armonic + 2a armonică (aproximare a formei de undă sawtooth).
componentele armonice ale undei pătrat
Semnalul dreptunghiular care cuprinde frecvența fundamentală plus un număr infinit de armonice impare. De exemplu, un semnal de undă pătrat la 1 kHz este compus din
valul fundamental de 1 kHz;
A treia armonică 3 * 1 = 3 kHz;
A 5 armonic 5 * 1 = 5 kHz;
armonicilor a 7 7 * 1 = 7 kHz, și așa mai departe. D.
Rețineți că oscilațiile complexe, care conțin doar armonici impare sunt în creștere abrupt margini și scade brusc taie. Armonicile mai ciudat cuprinde semnal, mai aproape forma sa de forma unui semnal dreptunghiular.
componentele armonice ale rampei
semnal Sawtooth include componenta fundamentală plus un număr infinit de armonici chiar. De exemplu, semnalul rampă la 1 kHz este compus din
valul fundamental de 1 kHz;
2a armonic 2 * 1 = 2 kHz;
4a armonic 4 * 1 = 4 kHz;
6a armonic 6 * 1 = 6 kHz, și așa mai departe. D.