o figură plan în jurul axei sale
Dana figura plan delimitat de linii. . .
1) Găsiți zona unei figuri plan delimitat de liniile de date.
2) Găsiți volumul solidul obținut prin rotirea unui figură plan delimitat de linii de date, în jurul axei.
Atenție! Chiar dacă doriți doar pentru a citi al doilea paragraf, mai întâi asigurați-vă că pentru a citi mai întâi!
Decizie. Sarcina este format din două părți. Să începem cu zona.
1) Efectuați desenul:
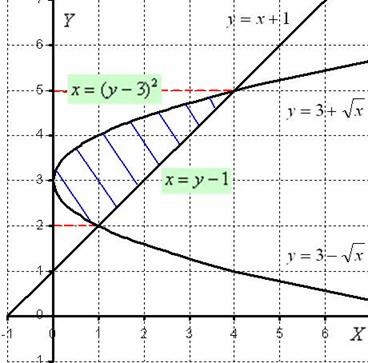
Este ușor de observat că funcția stabilește ramura superioară a parabolei, iar funcția - ramura inferioară a unei parabole. Înainte de a ne este parabole trivială că „culcat pe o parte.“
Cifra dorită, zona în care se găsesc, este umbrită în albastru.
Cum de a găsi zona cifra? Este posibil să se găsească o cale „normală“. Mai mult decât atât, zona cifra este suma pătratelor:
Există un mod mai rațional de a rezolva: ea constă în trecerea la funcțiile inverse și integrarea în raport cu axa.
Cum de a merge la funcțiile inverse? Aproximativ vorbind, este necesar să se exprime „X“ prin „y“. În primul rând, să se ocupe de un parabole:
Acest lucru este suficient, dar vedem că aceeași funcție poate fi derivată din ramurile inferioare:
SELF recomanda proiecte pe cale orală sau de substituție coordonate de 2-3 puncte în ecuația parabolei. acestea trebuie să satisfacă ecuația dată.
Cu totul mai ușor directe:
Acum ne uităm la axa. Vă rugăm să înclinați periodic capul spre dreapta cu 90 de grade în cursul unei explicații (nu este o glumă!). Cifra necesară se află pe segmentul. care este indicat prin linia punctată roșie. Astfel, pe segmentul de linie situată deasupra parabolei. și, prin urmare, zona a figurii trebuie să fie găsită pentru formula deja familiar. Ceea ce sa schimbat în formula? Numai scrisoarea, și nimic mai mult.
Pe segmentul. Prin urmare:
Observați cum am realizat integrarea, acesta este modul cel mai rațional, iar următorul pas de locuri de muncă este clar - de ce.
Pentru cititorii care se îndoiesc de corectitudinea integrării, vom găsi derivat:
Ia integrandul sursa, atunci integrarea este corectă.
2) calcula volumul corpului figurii formate prin rotirea în jurul axei.
Am Redesenați desen un design ușor diferit:
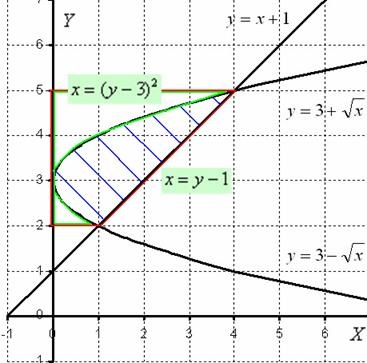
Deci, figura, albastru umbrită, se rotește în jurul unei axe. Rezultatul este „spânzurat Butterfly“, care se rotește în jurul axei sale.
Pentru a găsi volumul unui corp de rotație se va integra axial. În primul rând aveți nevoie pentru a merge la funcțiile inverse. Acest lucru a fost făcut și pictat în detaliu în paragraful precedent.
Acum ne înclina capul spre dreapta din nou și de a studia figura noastră. Evident, cantitatea de rotație a corpului trebuie să fie găsit ca diferența volumelor.
Rotiți figura, încercuite cu roșu, în jurul axei. rezultatul este un trunchi de con. Notăm acest volum de.
Rotiti figură, încercuit în verde, și în jurul unei axe notată cu volumul corpului rezultat al revoluției.
Domeniul de aplicare al fluture noastre cantități egale de diferență.
Folosind formulele pentru a găsi volumul unui corp de rotație:
Ceea ce este diferit de formula din secțiunea anterioară? Numai în scrisoarea.
Și aici este avantajul de integrare, pe care am vorbit recent, mult mai ușor de găsit. decât o pre-erecte integrandul în al patrulea grad.
Rețineți că, în cazul în care aceeași cifră plan este rotit în jurul unei axe. veți obține un corp complet diferit de rotație, cealaltă, desigur, volumul.
Se calculează volumul corpului format prin rotirea în jurul axei figurii delimitate de curbele și.
Decizie. Efectuați desen:
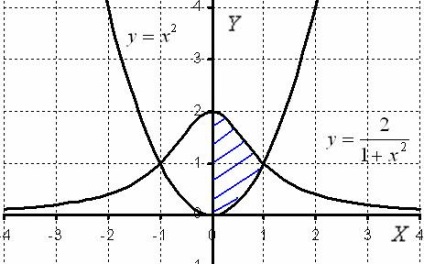
Pe drum, vom ajunge să cunoaștem listele de alte funcții. Aceasta este interesant graficul unei functii ....
În scopul de a găsi volumul unui corp de rotație este suficient pentru a utiliza jumătatea dreaptă a figurii, pe care am umbrit în albastru. Ambele funcții sunt chiar, graficele lor sunt simetrice față de axa. simetrică și figura noastră. Astfel, hașurate din partea dreaptă în timp ce se rotește în jurul axei. coincid în mod necesar cu partea stângă a negruntate.
Să ne întoarcem la funcțiile inverse, care este, exprimă „X-“ prin „y“:
Rețineți că ramura dreaptă a parabolei corespunde funcției inverse. Stânga ramură neutilizată a parabolei corespunde funcției inverse. În astfel de cazuri, de multe ori aveți dubii, ce ai alege o caracteristică? Îndoieli ușor spulberate, să ia orice punct al sucursalei drept și substituie coordonatele sale la funcția. Coordonate atins, atunci funcția stabilește exact ramura dreapta, nu stânga.
Apropo, aceeași istorie și funcțiile. Ceainicul, nu este întotdeauna clar imediat ce fel de funcție inversă pentru a selecta sau. De fapt, mă tem întotdeauna, înlocuind găsit o funcție inversă a unei perechi de puncte în grafic.
Acum, înclina capul spre dreapta și observați următorul lucru:
- pe un segment deasupra axei graficului este o funcție;
- pe un segment deasupra axei graficului este o funcție;
Este logic să presupunem că valoarea de rotație a corpului să caute mai mult ca suma volumelor solide de revoluție!
În acest caz: