6.2. Provocări pentru determinarea distanțelor dintre figuri geometrice
Distanța necesară în toate sarcinile acestui grup este măsurată prin lungimea segmentului, încheiat între formele geometrice predeterminate și perpendicular pe una dintre ele sau ambele la ambele. Acest segment este proiectat într-un segment congruentă ea cu planul de proiecție, care este perpendicular pe una sau ambele figuri geometrice, între care se determină distanța. Algoritmul pentru rezolvarea problemelor acestui grup este următoarea:
1. O metodă de conversie desen complex aduce ambele forme geometrice predeterminate (sau una dintre ele) într-o poziție perpendiculară pe un plan de proiecție.
2. Construiți lungimea dorită a proiecției pe acest plan.
Alegerea unei metode de conversie desen complexe în elaborarea algoritmului să ia în considerare cerințele pentru desen compactitatea, acuratețea și potențialul ușurința operațiilor grafice.
Sarcina 1 .Opredelenie distanta de la punctul M la linia AB în poziția generală (fig. 6.1). Distanța necesară măsurată prin lungimea segmentului / MN scăzut / perpendicular de la punctul M de pe linia AB. Segment [MN] se va proiecta într-un segment congruent pe un plan de proiecție perpendicular pe linia AB. Facem algoritmul de decizie:
1. Conversia liniei AB este proiectată în linie prin înlocuirea avionului de proiecție.
2. Construirea unui interval de proiecție [MN] la planul AB P5, N5 M5 a cărui lungime determină distanța dorită.
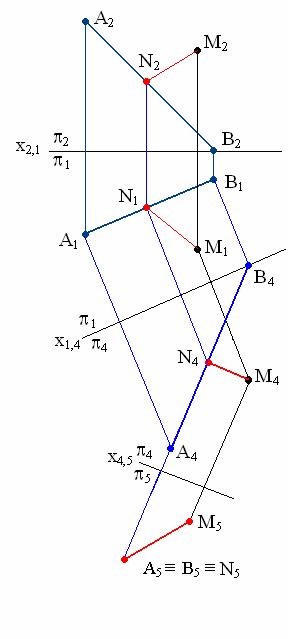
Fig. 6.1. Determinarea distanței de la punctul de la linia
Clădire. primă linie dreaptă AB este transformată într-un nivel de linie, atunci curba de nivel transformat într-o linie proiectată: două înlocuirea succesivă a planurilor de proiecție într-un proiectat implementat pentru transformarea liniei AB în poziția generală. Proiecțiile construite M4 și M5 din punctul M în sistemul P4 / P5.
Problema 2. Se determină distanța dintre liniile paralele a și b.
două substituții plan de proiecție trebuie să fie făcute pentru a rezolva problema. Inițial, liniile a și b trebuie să facă un nivel direct. Pentru a face acest lucru, P4 trebuie plasate paralel cu a1 și b1. Apoi, numit drept trebuie să fie poziționat perpendicular pe P5. Distanța dintre a5 și b5 este valoarea reală a liniilor drepte paralele a și b (fig. 6.2).
Sarcina 3.Opredelenie distanta de la punctul de la planul.
Soluția de rezolvare a problemei este prezentată în Fig. 6.3.
Pentru a determina distanța de la punctul M la planul triunghiului ABC δ nevoie plane δAVS triunghi generic convertite într-un plan proiectat. Pentru a face acest lucru, înlocuiți P2 plan de proiecție la P4 perpendicular pe H1.
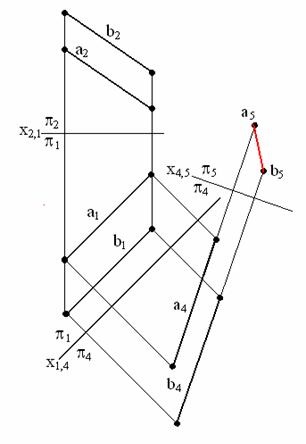
Fig. 6.2. Determinarea distanței dintre liniile paralele
δAVS avionul transformat într-o linie de A4 B4 C4. Pe același plan P4 va proiecta punctul M (M4). M4 perpendicular pe linia A4 B4 C4 Valoarea reală este distanța de la punctul M la ABC planul δ. Proiecțiile sunt transferate în plan perpendicular pe P1 și P2 liniilor de racordare corespunzătoare ale proiecției, distanța de la punctul M la planul δ ABC. Proiecțiile sunt transferate pe planul de proiecție perpendicular P1 și P2 a liniilor de comunicație respective.
Note: 1) Proiecția M1 N1 perpendiculară P1 este paralelă cu P4. deoarece P4 planul are dimensiunea sa reală.
2) Probleme 1- 3 poate fi rezolvată după cum urmează: se determină mai întâi proiecție deformată a metric lungimea dorită, și apoi o metodă triunghi dreptunghic pentru a determina valoarea sa reală.
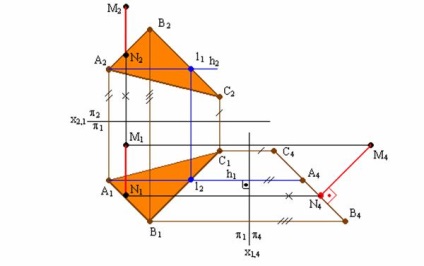
Fig. 6.3. Determinarea distanței de la punctul de la planul
Vă aducem revistele publicate de editura „Academia de Științe Naturale“
(Factor de impact ridicat RISC, teme reviste care acoperă toate domeniile științifice)