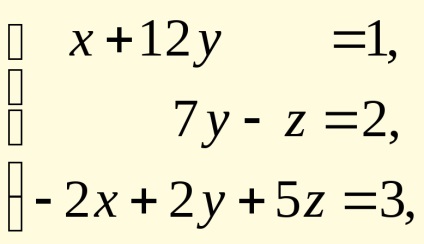LABORATOR DE LUCRU № 4
Diferențierea funcțiilor. semnificația geometrică a derivatului.
Scop. Aflați pentru a găsi valoarea numerică a funcției derivat într-un anumit punct.
Calcularea derivata unei funcții.
Mathcad operator de derivat pentru identificarea valoarea numerică a funcției derivat într-un anumit punct. Pentru a calcula cheia derivat este utilizat pentru a semna? .
În scopul de a găsi derivata funcției și calculează valoarea sa numerică, trebuie să faceți următoarele:
În primul rând, se determină punctul în care doriți să găsiți derivatul.
Faceți clic pe definițiile de mai jos acest punct. Apoi formați. Acesta va fi operatorul derivatului cu două domenii:
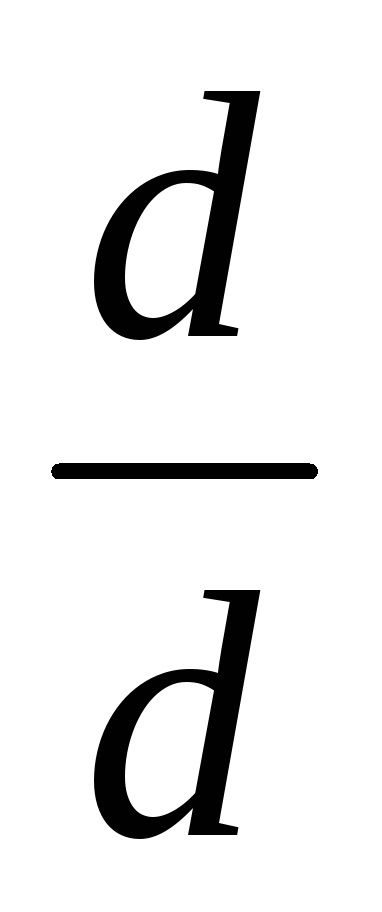
Dați clic pe câmpul de la numitor și tastați numele variabilei pe care diferențierea se realizează.
Faceți clic pe câmpul din dreapta
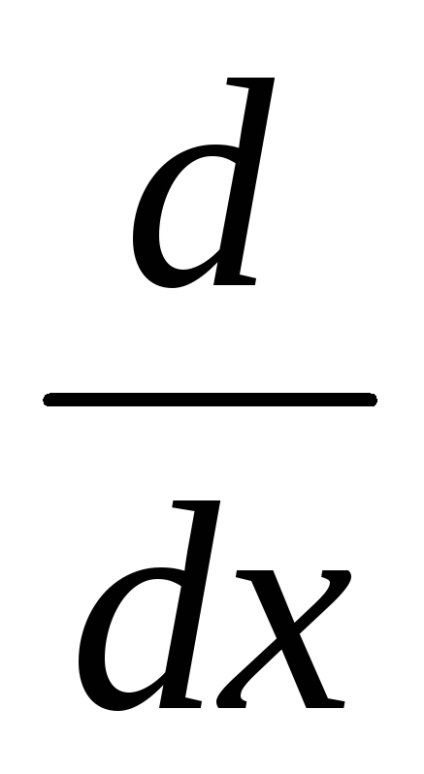
Pentru a vedea rezultatul, apăsați = semnul.
Sarcina 1.1 Găsiți derivata în punctul
Definim punctul în care doriți să găsiți derivatul:
Introducem operatorul derivat, câmpurile și se calculează derivatul:
* Rezultatul diferențierii nu este o funcție și numărul - valoarea derivatului la un moment dat al variabilei diferențiere.
Deși diferențierea returnează un singur număr, puteți defini o funcție la alta functie ca un derivat. De exemplu:
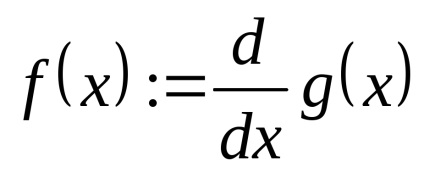
Calculul f (x) se va întoarce într-o formă numerică derivat g (x) la x.
Expresia care urmează să fie diferențiate, poate fi real sau complex.
diferențierea variabilă ar trebui să fie simplă variabilă non-indexată.
semnificația geometrică a derivatului.
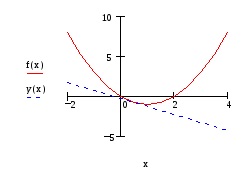
Sarcina 1.2. Funcția Dana at = f (x). Se trasează funcția tangentă și graficul de la punctul cu abscisa x = x0, dacă - ecuația tangentei.
Introducem această funcție și să găsească valoarea sa la punctul:
Să ne găsim derivata acestei funcții în punctul:
Ecuația tangentei la această funcție:
Noi construim graficul funcției și tangenta la ea.
Ținte 3. Se efectuează calcule diferențiale în formă simbolică:
Sarcina 4. Găsiți derivata funcției în orice punct.
Scop. Învață să găsiți integralele definite de funcții pentru a calcula aria unei figuri cu ajutorul integralei.
integrarea operatorului Mathcad pentru calculul numeric al unei funcții integrala definită peste un interval.
semnul integrală este afișat atunci când apăsați butonul cu semnul .
Pentru a calcula definită integral, trebuie să faceți următoarele:
Dați clic pe semnul zonă și de tip gol . Vei vedea semnul integrală cu câmpuri goale pentru integrandul, limitele de integrare și variabila de integrare: ∫
Faceți clic pe caseta din partea de jos și scor limita inferioară de integrare. Dați clic pe tipul câmpului superior și limita superioară de integrare.
Dați clic pe câmpul dintre semnul integral și d și tastați expresia pe care doriți să se integreze.
Dați clic pe ultimul câmp gol și introduceți variabila de integrare.
Pentru a vedea rezultatul, apăsați = semnul.
Introducem semnul integral și completați câmpurile;
* Limitele de integrare trebuie să fie reale. Expresia care urmează să fie integrate pot fi reale sau complexe. variabilă de integrare în plus, toate variabilele din integrandul ar trebui să fie definite anterior în altă parte documentul de lucru. Variabila de integrare ar trebui să fie o simplă variabilă fără un index. În cazul în care variabila de integrare este o cantitate dimensionala, limitele superioare și inferioare de integrare trebuie să fie de aceeași dimensiune.
forme pătrate. După cum se cunoaște, prin intermediul unei integrale poate fi definit zona cifra calculată.
Noi construim graficele acestor funcții într-o singură cutie de imagine:
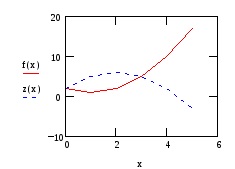
Se calculează aria cifra rezultată:
Sarcina 2.1. Rulați calcul integrală în formă simbolică:
Sarcini 3.1 Se calculează precis integrală.
Sarcina 3.2. Găsiți zona cifra delimitată de graficele funcțiilor. Pentru a construi această cifră.
Sistem de ecuații liniare
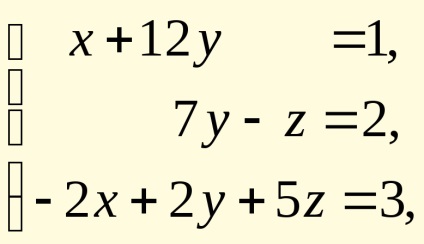
în care raporturile matricei pătrate a necunoscutele
, și membrii liberi într-o matrice, puteți
scris ca o ecuație matrice, unde există o matrice coloană de necunoscutele. Coloana este necunoscută din ecuația matriceală prin multiplicarea pieselor lăsate de matricea inversă, care există numai dacă determinantul sistemului este diferit de zero. Rezultatul (din. În cazul în care matricea de identitate). Această metodă de rezolvare a sistemului de ecuații liniare se numește metoda de matrice. În cazul nostru, obținem (numeric și simbolic)
Testați soluția constă în înlocuirea soluției găsite în ecuația matrice, care, în acest caz, ar trebui să se aplice adevărata egalitate. Ca rezultat al substituției obținem:
3.1. Găsiți determinantul unei matrice, iar transpusa inversă a matricei.
matrice 5x5 alcătuiesc propriile lor.
3.2. Rezolva sistemul de ecuații liniare folosind metoda matricei.