Patrulaterul este un poligon, care topuri $ 4 $.
Patrulaterul are laturile $ 4 $, 4 $, $ 4 și $ $ unghi la vârf. Părțile care nu au noduri comune, numit pe partea opusă a patrulaterului, în caz contrar acestea se numesc adiacente. Unghiurile nu au părți comune, de asemenea, denumite adiacente.
Noi acum direct, definiția unui paralelogram.
Paralelogramul - un patrulater în care laturile opuse sunt paralele unele cu altele.
Să ne amintim proprietățile de bază ale unui paralelogram.
Proprietatea 1: laturile opuse și colțuri ale paralelogramului, respectiv, sunt interconectate.
Proprietatea 2: realizată în diagonală paralelogram bisect punctul lor de intersecție.
Luați în considerare alte concepte detaliu dreptunghi, romb și pătrat.
dreptunghi
Paralelogram, care are un unghi drept, se numește un dreptunghi (Fig. 1).
Figura 1. dreptunghi
Evident, în caseta de la toate cele patru colțuri sunt egale cu $ ^ 0 $
Luați în considerare următoarele două proprietăți ale dreptunghiului.
Proprietatea 3: Atât diagonala unui dreptunghi sunt egale.
Să se dea un pătrat $ ABCD $. Desenați-diagonală $ $ AC și $ BD $ (Fig. 2). Demonstrăm că $ AC = BD $.
Din moment ce, prin definiție, un dreptunghi $ 1 $ este un paralelogram, atunci proprietatea $ 1 $ paralelogram, avem
Deoarece $ \ unghiul B = \ unghi A = ^ 0 $ și $ AB $ - partea comună, apoi, pe baza egalității de triunghiuri I, $ \ triunghi ABD = \ triunghiul ABC $. prin urmare
Proprietatea 4 (caracteristica dreptunghi): Dacă cele două diagonalele paralelogramului sunt egale, atunci este un dreptunghi.
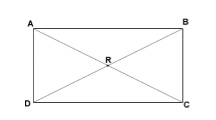
Să se dea un pătrat $ ABCD $. Am diagonala $ $ $ AC și BD $ trage. Să-i întâlnesc într-un punct $ R $ (fig. 2).
De la proprietatea $ 2 $ o egalitate paralelogram și diagonalele sale, obținem
$ \ Unghi Deoarece RDC = \ unghi ARB $, ca pe verticală, atunci $ I $ baza egalității de triunghiuri $ \ triunghi RDC = \ triunghi ARB $. Deci, $ \ unghi RDC = \ unghiul RCD = \ unghiul RAB = \ unghiul RBA $.
Deoarece $ AB = AD $, atunci triunghiul $ $ ABD este isoscel, precum și un $ AE $ - triunghi Median $ ABD $, $ AC $ este perpendicular $ BD $.
Dreptunghi unde toate cele patru laturi sunt egale între ele, numită pătrat (fig. 5).
Figura 5. Piața
Pătratul - un caz special al unui romb. În consecință, piața are toate proprietățile unui dreptunghi și romb.
de exemplu, problema
Găsiți perimetrul pătrat, a cărui diagonală este de $ 10 $.
Notăm parte a pieței de $ o $. Apoi, în conformitate cu teorema lui Pitagora