Definiția. Doi avion nazyvayutsyaparallelnymi. în cazul în care nu se intersectează.
Figura prezintă un plan paralel.
Poziția relativă a celor două planuri în spațiu: două planuri în spațiu, fie au un punct comun, și anume, se intersectează sau sunt disjuncte, adică, paralel.
Simptom două planuri paralele.
Teorema. Dacă două linii drepte care se intersectează paralele cu același plan, respectiv la două unghiuri drept un alt plan, atunci aceste planuri sunt paralele.
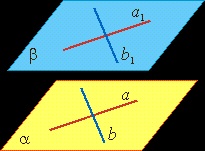
Proprietățile de planuri paralele.
Proprietatea 1. În cazul în care două planuri paralele sunt străbătute de o treime, acestea sunt paralele cu linia de intersecție.
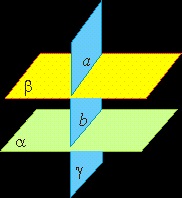
Proprietate 2. Secțiunile de linii paralele încheiate între planuri paralele sunt egale.
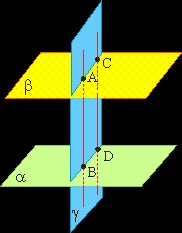
Proprietatea 3. În cazul în care linia intersectează planul, traversează, de asemenea, orice plan paralel cu acest lucru.
Proprietatea 4. În cazul în care planul intersectează unul dintre planurile paralele, apoi traversează și alte.
Proprietatea 5. Prin punctul nu se află în planul se extinde paralel cu acest plan și numai unul.
Proprietatea 6. În cazul în care două planuri sunt paralele cu a treia, atunci ele sunt paralele între ele.
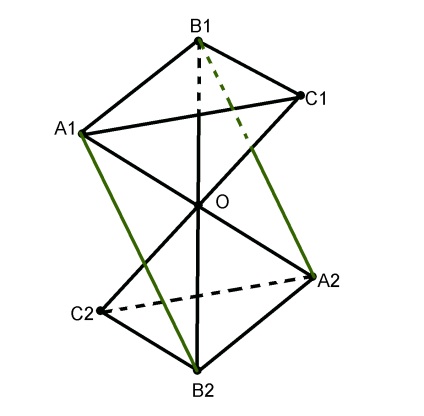
Trei segmente, și care nu se află în același plan, au un mijloc comun. Demonstrati ca ploskostiiparallelny.
Să punctul O- de intersecție a segmentelor și. Luați în considerare patrulater. Acest diagonaliitochkoy dreptunghi intersecție împărțită în jumătate, și apoi paralelogram pryamougolnik-. Apoi storonyiparallelny.
Sa dovedit a fi în mod similar și paralelism.
Ca urmare, descoperim că cele două linii care se intersectează iparallelny două linii intersectate, apoi pe baza paralelism a două avioane ploskostiiparallelny.
întrebări de control și sarcini:
Punctul B nu se află în planul treugolnikaADC. tochkiM, N. iP - mijlocul anului otrezkovBA, respectiv BC BII.
Demonstrati ca MNP IADC plan paralel.
Găsiți zona triunghiului MNP. în cazul în care zona treugolnikaADC este de 48.
segmente paralele izaklyucheny între ploskostyamii paralele.
Se determină tipul de patrulatere, și.
Trei linii care trece printr-un singur punct și nu se află într-un singur plan, traversează una dintre planuri paralele la punctele și, iar celălalt - în punctele și. Demonstrati ca treugolnikiipodobny.