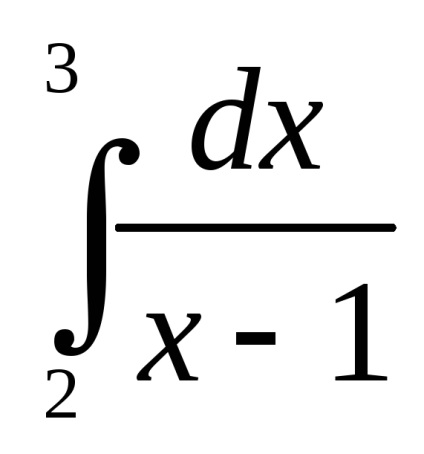Pentru a calcula un integral integrat
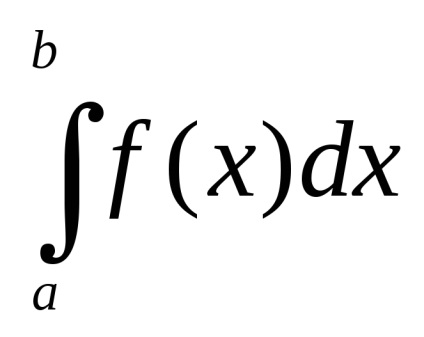
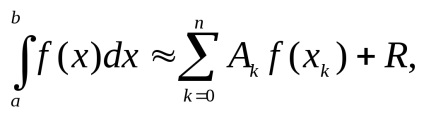
unde xk și Ak sunt determinate prin formula de cvadratură, R este restul termenului sau eroarea formulării de cvadratură.
Segmentul de integrare [a, b] este împărțit în n părți egale de un sistem de puncte echidistant xi = x0 + ih. unde i = 0,1,2. n; x0 = a, xn = b.
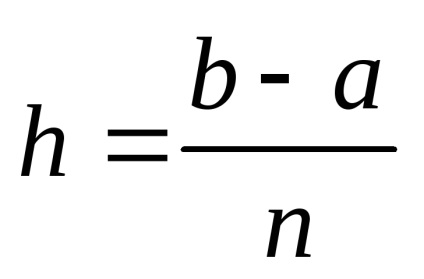
Formulele de cvadratură pentru nodurile echidistant:
1) formulei dreptunghiurilor stângi:
unde yi = f (xi), xi = a + ih;
2) formula dreptunghiurilor drepte:
unde yi = f (xi), xi = a + ih;
3) formula dreptunghiurilor centrale:
unde yi = f (xi),
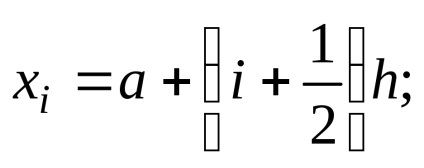
4) formula trapezoidală:
unde yi = f (xi), xi = a + ih;
5) Formula lui Simpson (formula parabola):
unde yi = f (xi), xi = a + ih.
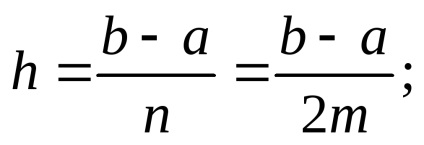
6) Formula lui Newton (regula
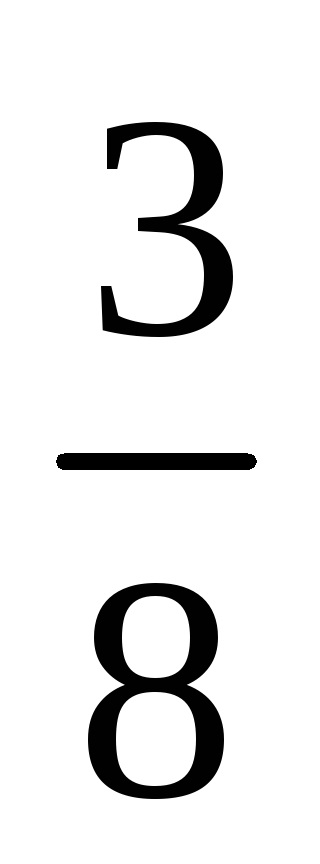
unde yi = f (xi), xi = a + ih.
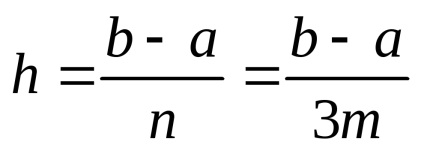
Integralele sunt considerate cu formule de cvadratură cu precizie . Pentru a obține precizia necesară a calculului . se folosește metoda dublării. Integolul se calculează de la formula de cvadratură aleasă de două ori, mai întâi cu o anumită etapă h. apoi în trepte
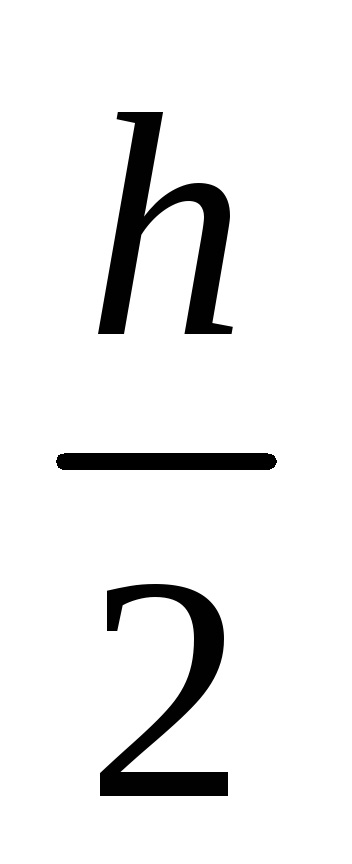
Denumim rezultatele partițiilor Jn și respectiv J2n și le comparăm. Dacă | Jn-J2n |<. где – погрешность вычислений, то в качестве результата берут J2n . Если |Jn-J2n|. то вычисления повторяют с шагом
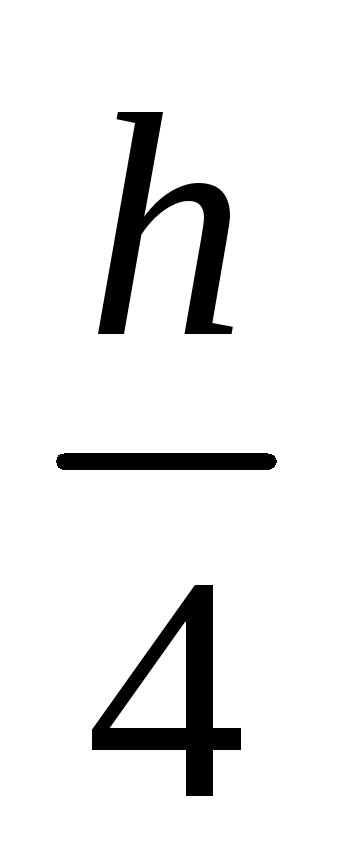
Un exemplu. Folosind formula trapezoidală, calculați integralele