Dacă două corpuri oscilează cu aceeași frecvență și în orice moment dat sunt în aceeași stare în raport cu poziția de echilibru, astfel oscilații apar în aceeași fază.
Un exemplu. a suspendat două penduluri identice și a scos în același timp pozițiile de echilibru
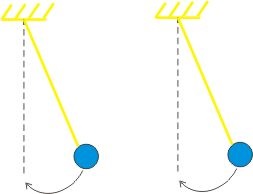
Dacă două corpuri oscilează cu aceeași frecvență și una dintre ele repetă toate stările celuilalt cu o anumită întârziere de timp, atunci aceste oscilații apar cu o schimbare de fază.
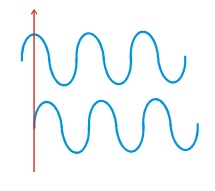
Un exemplu. au atârnat două penduluri identice și au fost eliberate la momente diferite.
Dacă două corpuri oscilează cu aceeași frecvență, dar în același timp se mișcă în direcții opuse tot timpul, atunci oscilațiile apar în faze opuse.
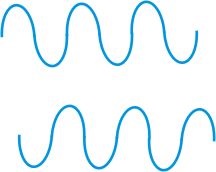
Un exemplu. Două penduluri de aceeași lungime sunt respinse la unghiuri egale, dar în direcții opuse.
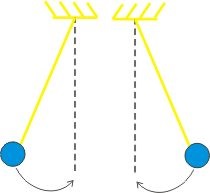
Valoarea sub semnul sinusoidal sau cosinus este faza oscilațiilor (unitatea de măsură este radiana).
Faza determină, pentru o anumită amplitudine, starea sistemului oscilant în orice moment (coordonate, viteză, accelerare).
Raportul indică care parte a perioadei a trecut de la începutul oscilațiilor. Orice valoare a timpului, exprimată în fracții ale perioadei, corespunde valorii fazei, exprimată în radiani.
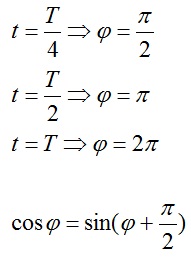
Prin urmare, în locul formulei, putem folosi echivalentul
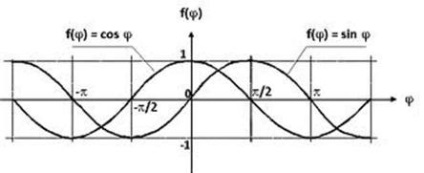
Graficele funcțiilor y = cos x y = sin x sunt deplasate în fază cu / 2.