Orei bune a zilei, harbachitatel.
Formularea problemei
Există o serie de puncte Y situate uniform pe axa X. Trebuie să obțineți un grafic neted ce trece prin toate punctele date. Exemplu în imaginea de mai jos:
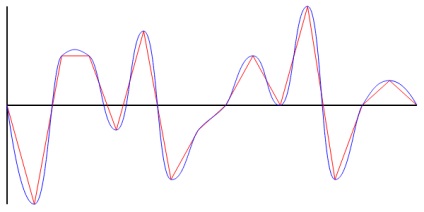
Toți cei care sunt interesați, întreabă sub tăiere.
Există o serie de soluții standard, pentru o curbă lină prin punctele (în acest sens, o mulțime de lucruri interesante scrise în articolul menționat deja), cum ar fi, de exemplu, interpolare spline. Atunci când al treilea curs a fost inventat acest algoritm, cuvântul „interpolare“, mă umple de groază, și gugleniya la cerere „netezirea grafice“ nu a dat rezultate în puterea de înțelegere. Dar cumva am ajuns la curbele Bezier și mi-a plăcut cu adevărat. Trage rapid, algoritmul este intuitiv ... Ce altceva este necesar pentru fericire. Păi, într-un fel a concurat.
Ideea principală
Voi sparge ideea în trei paragrafe pentru ao face mai ușor de înțeles și mai ușor de citit.
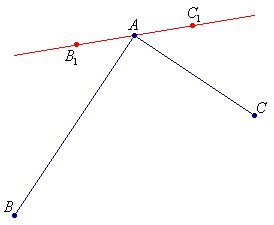

Astfel, se pare că problema este redusă la căutarea liniei drepte (B1 C1) și, de fapt, la punctele de referință B1 și C1. pe care vom construi mai târziu curbele Bezier.
Căutați o adresă directă
După cum se știe, linia din plan este exprimată prin formula y = kx + b. unde k este panta pantei liniei la axa X. Cand gasim k. atunci știind că linia dreaptă trece prin punctul A. și știind coordonatele sale, putem găsi cu ușurință b. b = YA-kXA. Astfel, totul se rezumă la găsirea coeficientului k.
Căutați coeficientul k
Am spus dinainte că k = tg (φ) = tg ((α-β) / 2) = (sqrt ((2 + Ax (YA -YB) 2) * (2 + Ax (YA -YC) 2)) - dx 2 - (YA -YB) * (YA -YC)) / (* Ax ((YA -YB) - (YA -YC))). unde ΔX este distanța în X între puncte (îmi amintesc că punctele noastre sunt distribuite uniform pe X). Mai jos este o dovadă matematică a corectitudinii formulării, dar dacă nu sunteți în starea de spirit, puteți să o ignorați.
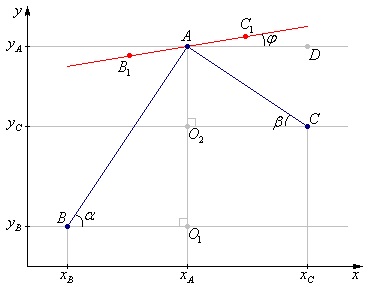
Determinarea matematică a coeficientului k
(7) ∠DAC = ∠O2 CA = β - ca unghiuri versatile interne formate de două linii paralele (AD) și (O2 C) și secant (AC)
Prin paranteze pătrate se înțelege lungimea segmentului (nu am vrut să folosesc linii drepte verticale - sper că cititorul mă va ierta)

Și așa, k am găsit; b știm de asemenea (vezi mai sus) și astfel linia pe care se află punctele de sprijin este cunoscută de noi.
Căutăm puncte de referință
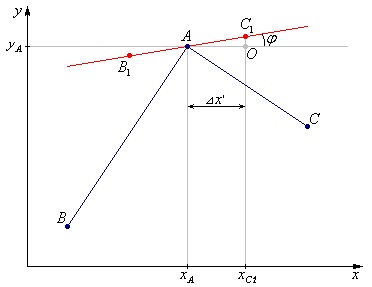
Un pic de matematică, ceea ce dovedește asta
Din trigonometrie, ne amintim că:
Dacă luăm [AC1] egal cu jumătate din pasul în X între punctele principale ale graficului (punctele B și A. A și C. etc.), atunci:
Pentru plăcere!
Exemplu de implementare pe JSFiddle