Metoda de calcul se bazează pe următoarea idee:
- Un cerc cu o rază a unității este înscris într-un pătrat cu partea a doua.
- Formăm coordonatele unui punct aleatoriu (aruncăm un grăunte de nisip într-un pătrat dat, o pietricică). Această "aruncare" aleatorie și metoda conexă cu capitalul jocurilor de noroc, unde totul este construit și pe întâmplare.
- Un punct poate cădea într-un cerc sau nu (starea de succes: x 2 + y 2 <= 1)
- Numărăm numărul de hit-uri Np pentru un număr suficient de mare de aruncări N.
- Dacă punctele sunt aleatoare, atunci raportul punctelor găsite la numărul total de încercări este egal cu raportul dintre zonele cercului și pătrat. Np / N = Scr / Sqn = πR2 / (2R) 2
- Numărul π = 4 · Np / N
Programul despre "pur" Pascal arată astfel:
Precizia calculului depinde de numărul de încercări (numărul n).
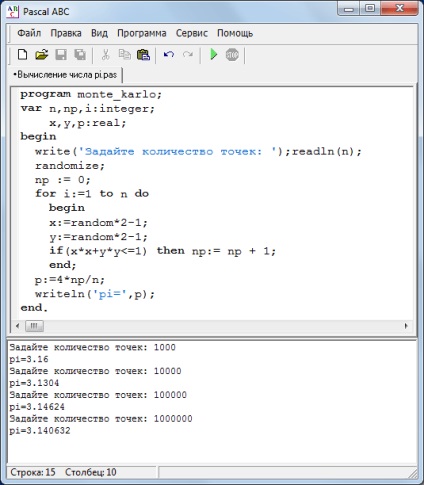
calculând numărul pi pentru un număr diferit de încercări
Pentru a realiza partea vizuală în Lazăr aveți nevoie de coordonate carteziene ocazionale sunt convertite în ecran, precum și în articolul: Trasarea funcții Lasarus. Aplicația include componente TImage pentru câmpul de introducere a imaginii, un buton, și mai multe de imprimare:
Un punct aleatoriu cu coordonatele x, y (numerele reale din intervalul (-1; 1) sunt traduse în coordonatele ecranului:
xd: = rotundă (x0 + x * r);
yd: = rotund (y0 + y * r);
unde r este lungimea unui singur segment în pixeli.
Punctul este vopsit folosind următoarea metodă: Form1.image1.Canvas.Pixels [xd, yd]: = clBlue;
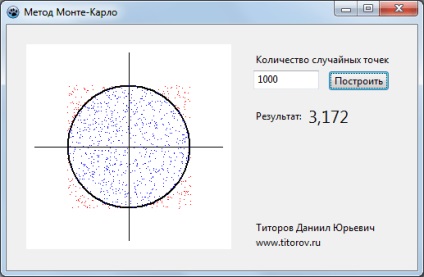
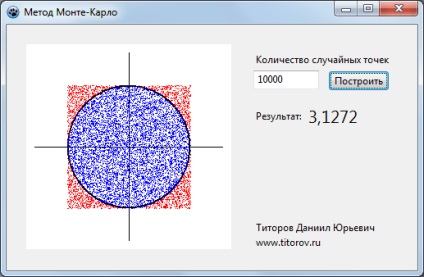
10 000 de puncte aleatoare. Precizia calculului este mai mare.
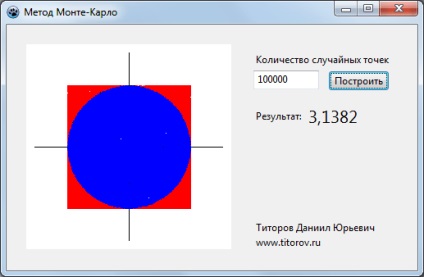
Este ușor de văzut precizia obținută numai cu un număr suficient de mare de fotografii. De asemenea, precizia este determinată de calitatea generatorului de numere aleatorii.