Obiectiv: să învețe să rezolve problemele aplicate cu ajutorul unui derivat.
Exemplu de îndeplinire a sarcinilor
1. Organismul se deplasează rectiliniu conform unei legi date.
a. Găsiți viteza instantanee a corpului în momentul de timp.
b. Găsiți accelerația corpului în momentul momentului unei secunde.
c. Găsiți, după câte secunde de la origine, viteza instantanee a corpului va fi = 44m / s.
d. Aflați, după câte secunde de origine, accelerația corpului va fi egală.
a) Pentru a găsi viteza, calculăm derivatul de ordinul întâi. Apoi, viteza instantanee în 1 secundă.
b) Pentru a găsi accelerația, calculați al doilea derivat. Apoi, în 2 secunde va fi accelerarea.
c) Pentru a determina timpul după care viteza corpului va fi de 44 m / s, este necesară rezolvarea ecuației. Avem t = 2 secunde.
d) Pentru a determina timpul după care accelerația corpului este de 22 m / s 2, este necesară rezolvarea ecuației. Rămâne să găsim t.
Rețineți că dacă în versiunea dvs. există o liniuță în coloana corespunzătoare, atunci acest element nu este necesar.
2. Desenați ecuația tangentei în graficul funcției
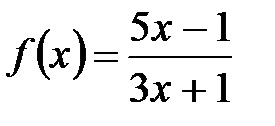
Prin ipoteza problemei x0 = 1 și f (x0) = f0 = 1. Ecuația tangentei are forma
.
Astfel, rămâne de găsit
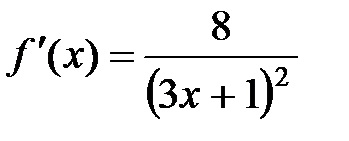
Apoi ecuația tangentei ia forma
1. Corpul se deplasează rectiliniu conform unei legi S (t).
a. Găsiți viteza instantanee a corpului la un moment dat.
b. Găsiți accelerația corpului la un moment dat.
c. Găsiți, după câte secunde de la origine, viteza instantanee a corpului va fi egală cu.
d. Aflați, după câte secunde de origine, accelerația corpului va fi egală.
Corpul se deplasează rectiliniu conform legii S (t)