Prisma este descrisă în apropierea cilindrului, dacă bazele sale sunt poligoane descrise în apropierea bazei cilindrului. În consecință, cilindrul este înscris în prisma.
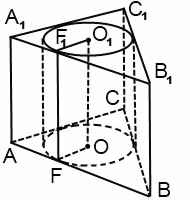
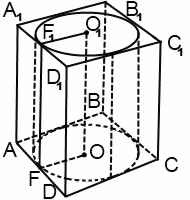
Cilindrul poate fi înscris în prism dacă un cerc poate fi înscris în baza prismei. Raza cercului înscris este egală cu raza cilindrului. Înălțimile cilindrului și a prismei sunt egale. În cursul școlii se studiază doar un cilindru circular drept, respectiv, cilindrul, în acest caz, este înscris într-o prismă dreaptă.
Fețele laterale descrise în apropierea cilindrului de prisme sunt plane tangente față de suprafața laterală a cilindrului.
Să găsim raportul dintre volumul prismei și volumul cilindrului înscris în el:
p - semiperimetrul prismă de bază, r - raza cercului inscris la baza unei prisme și raza cilindrului, H - înălțimea prismei și înălțimea cilindrului.
În special, raportul dintre volumul prismei triunghiulare regulate și volumul cilindrului inscripționat
Raportul dintre volumul unei prisme cvadrangulare regulate și volumul unui cilindru inscripționat
Pentru o prismă hexagonală regulată, acest raport este
Raportul dintre suprafața laterală a prismei și suprafața laterală a cilindrului inscripționat:
Deoarece jumătate din perimetrul bazei este o jumătate de perimetru,
Astfel, dacă cilindrul este introdus în prisma, raportul ariei suprafeței laterale a prismei pe suprafața laterală a cilindrului este egală cu prismă în raport cu volumul cilindrului inscris. În particular, raportul dintre suprafața laterală a prismei triunghiulare regulate și suprafața laterală a cilindrului inscripționat
Raportul dintre suprafața laterală a prismei cvadrangulare obișnuite și suprafața laterală a cilindrului inscripționat
Raportul dintre suprafața laterală a prismei hexagonale regulate și suprafața laterală a cilindrului inscripționat
Pentru rezolvarea problemelor în care cilindrul este înscris în prisma, se poate considera o parte din secțiunea transversală a combinației de corpuri printr-un plan care trece prin axa cilindrului. Pentru o prismă directă, această secțiune este un dreptunghi ale cărui laturi sunt egale cu raza cilindrului și înălțimea cilindrului. De exemplu, AA1O10: AA1 = H, AO = r.