Soluția de inegalități trigonometrice cu tangență, matematică-repetiție

3. Gasiti intervalul valorilor t. sub care tangenta este situata sub linia dreaptă y = a. Limita stânga a acestui interval este întotdeauna (-π / 2). și arctul drept a

4. Notați dubla inegalitate pentru argumentul t. ținând seama de perioada tangentă T = π (t va fi între abscise (-π / 2) și arctg a).

5. Facem o substituție inversă (revenim la argumentul original) și exprimăm valoarea lui x din dubla inegalitate, scriem răspunsul sub forma unui interval numeric.

Soluția de inegalități trigonometrice ne asigură în mod grafic în mod fiabil împotriva erorilor numai dacă construim corect grafice.

Construim grafice ale funcțiilor y = tgx și y = 1. Să analizăm în detaliu construcția unui tangentoid. Să pregătim planul de coordonate xOy după cum urmează:

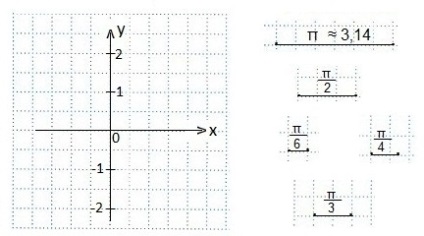
segmentul unitar este egal cu două celule; din moment ce valoarea lui ≈ 3,14. atunci π pe axa orizontală Ox va fi reprezentată de șase celule; jumătate π (acesta este π / 2) - trei celule. O celulă este π / 6; una și jumătate de celule sunt π / 4; două celule vor corespunde argumentului π / 3.

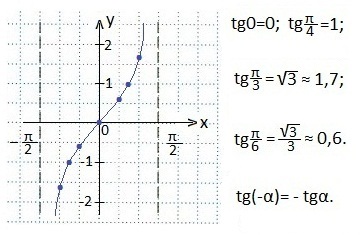
Știm că tangenta de 90 ° nu există și deoarece funcția tangentă este periodică cu cea mai mică perioadă egală cu π. atunci nu există nici o tangentă (90 ° + πn). Luăm în considerare acest lucru în construirea graficului și efectuarea a două asimptote. x = - π / 2 și x = π / 2.

Astfel, în intervalul de la - π / 2 la π / 2, tangenta va "trece prin" toate valorile sale. Folosind valorile tangente ale unor unghiuri și caracterul ciudat al funcției tangente (graficul va fi simetric în raport cu originea), vom construi puncte în planul de coordonate pregătit prin care facem tangentoidul.

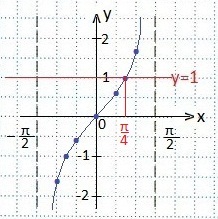
O tragem paralel cu axa Ox. mai mare cu un interval de unitate (până la 2 celule).

Linia dreaptă y = 1 intersectează tangentoidul în punctul cu coordonatele (π / 4; 1).

Se determină intervalul valorilor lui x pentru care inegalitatea este adevărată, adică în interiorul căreia tangenta este situată sub linia dreaptă y = 1. Luăm în considerare faptul că inegalitatea nu este strictă, prin urmare, capătul din dreapta al intervalului (π / 4) este inclus în setul de soluții ale inegalității. Scriem soluția sub forma unei inegalități duble. Răspunsul este scris sub forma unui decalaj.

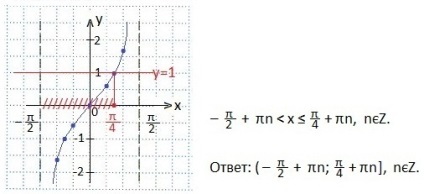
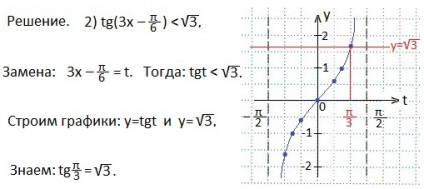
Notați intervalul valorilor lui t. pentru care punctele tangentei sunt sub punctele liniei drepte y = 1. Să scriem acest interval sub forma unei inegalități duble. Apoi îl vom suprascrie pentru argumentul original și vom exprima x. Răspunsul este scris sub forma unui decalaj.

Se marchează intervalul valorilor lui t. sub care inegalitatea este adevărată. Avem o inegalitate nestrictă, ceea ce înseamnă că sfârșitul corect al intervalului de valori t este de asemenea o soluție la inegalitate. Ne întoarcem la argumentul original și exprimăm x. Răspunsul este scris sub forma unei game de valori a variabilei x.

Articole similare